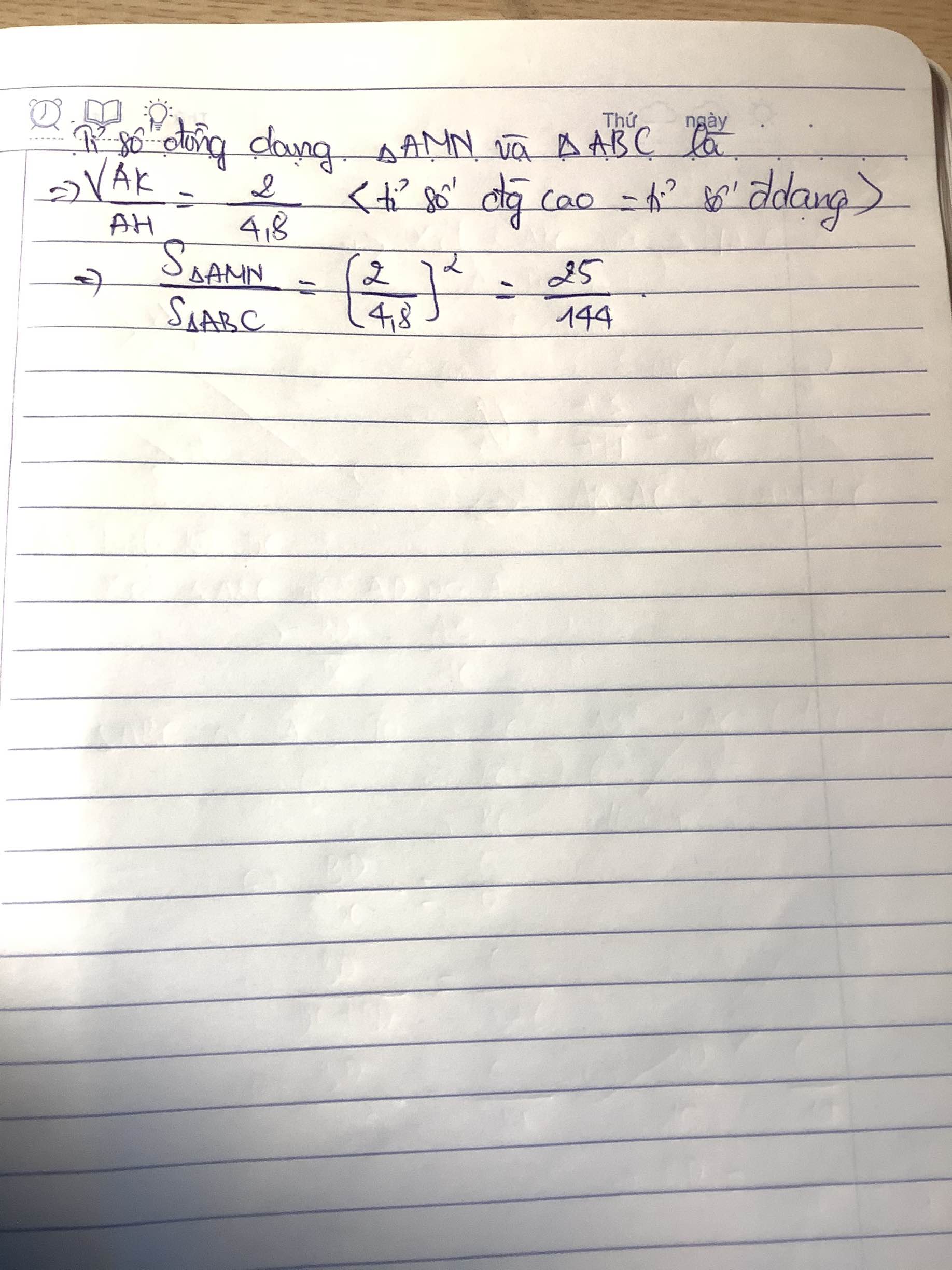Cho tam giác ABC vuông tại A, có AB AC. Vẽ AH ⊥ BC (H ∈ BC)a) Chứng minh: ∆HBA ∽ ∆ABCb) Tính độ dài các cạnh BC và AH nếu AB 9cm, AC 12cmc) Trên cạnh HC lấy điểm M sao cho HM HA. Qua M vẽ đường thẳng vuông góc với cạnh BC cắt AC tại I. Qua C vẽ đường thẳng vuông góc với cạnh BC cắt tia phân giác của tại K. Chứng minh ba điểm H, I, K thẳng hàngCho tam giác ABC vuông tại A, có AB AC. Vẽ AH ⊥ BC (H ∈ BC)a) Chứng minh: ∆HBA ∽ ∆ABCb) Tính độ dài các cạnh BC và AH nếu AB 9cm, AC 12cmc) Trên cạ...
Đọc tiếp
Cho tam giác ABC vuông tại A, có AB < AC. Vẽ AH ⊥ BC (H ∈ BC)
a) Chứng minh: ∆HBA ∽ ∆ABC
b) Tính độ dài các cạnh BC và AH nếu AB = 9cm, AC = 12cm
c) Trên cạnh HC lấy điểm M sao cho HM = HA. Qua M vẽ đường thẳng vuông góc với cạnh BC cắt AC tại I. Qua C vẽ đường thẳng vuông góc với cạnh BC cắt tia phân giác của tại K. Chứng minh ba điểm H, I, K thẳng hàng
Cho tam giác ABC vuông tại A, có AB < AC. Vẽ AH ⊥ BC (H ∈ BC)
a) Chứng minh: ∆HBA ∽ ∆ABC
b) Tính độ dài các cạnh BC và AH nếu AB = 9cm, AC = 12cm
c) Trên cạnh HC lấy điểm M sao cho HM = HA. Qua M vẽ đường thẳng vuông góc với cạnh BC cắt AC tại I. Qua C vẽ đường thẳng vuông góc với cạnh BC cắt tia phân giác của tại K. Chứng minh ba điểm H, I, K thẳng hàng







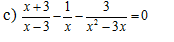

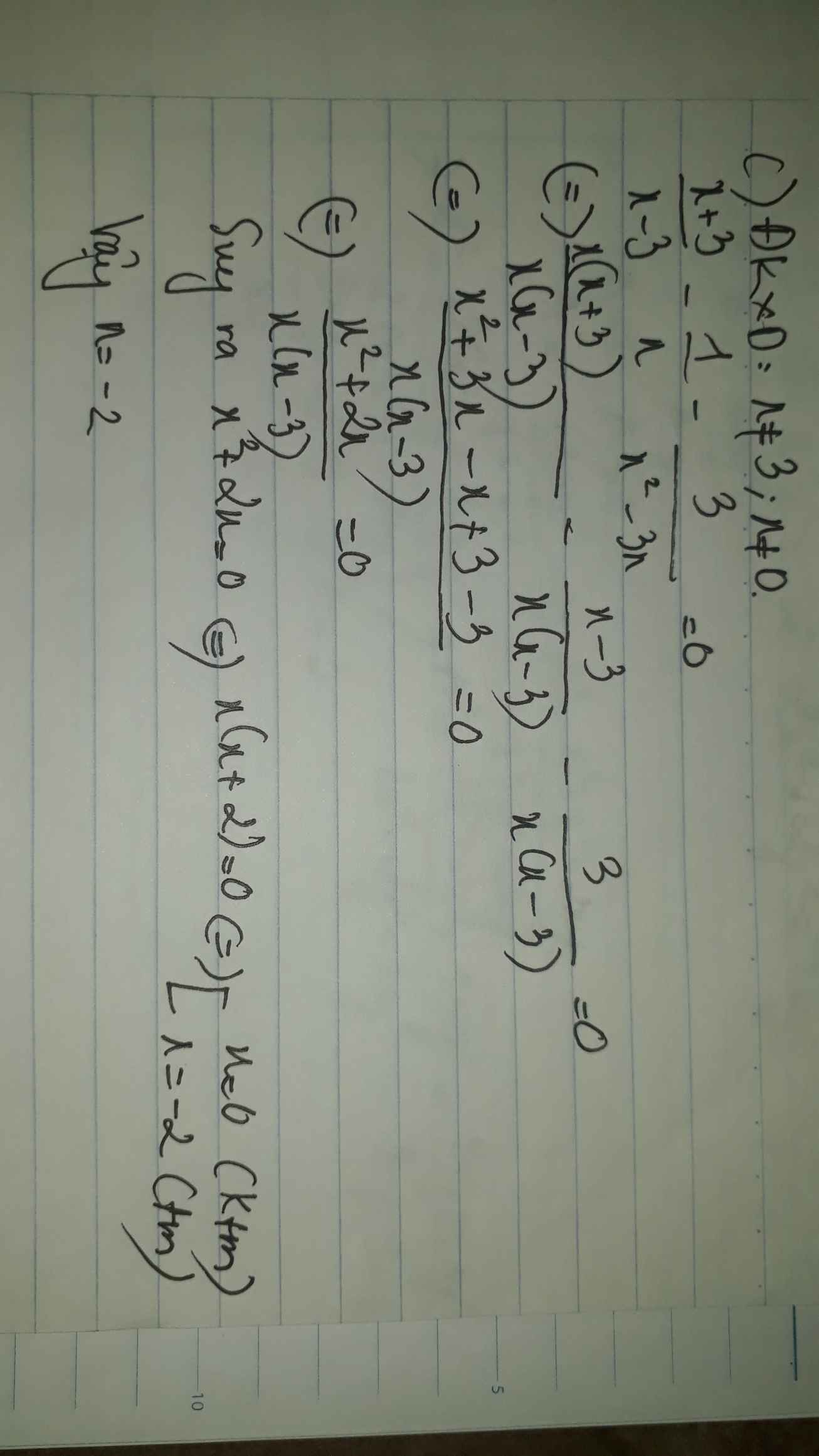


 :>
:>