Đa giác. Diện tích của đa giác
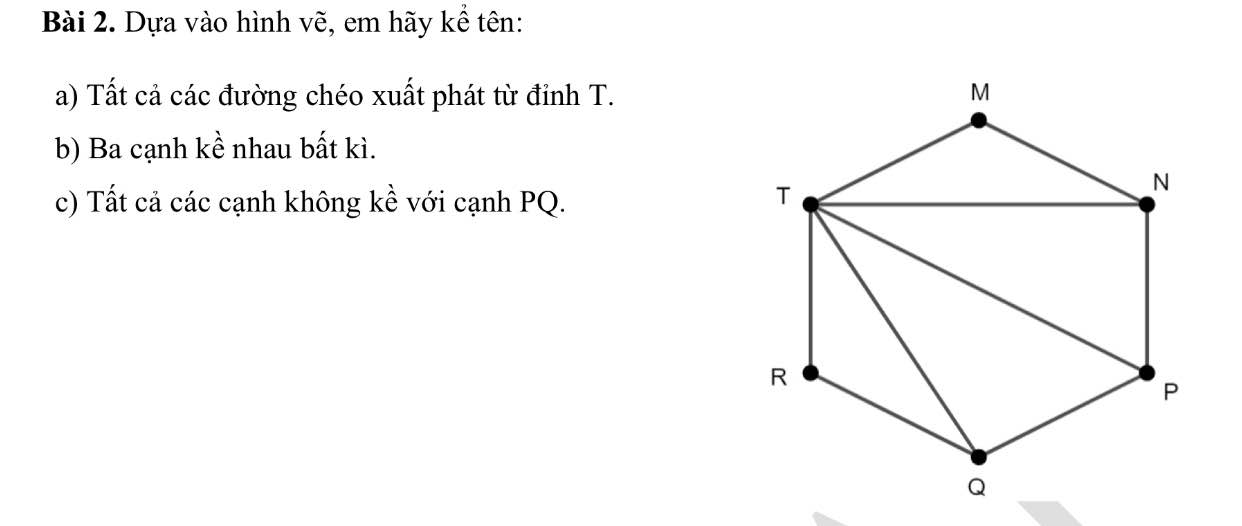
`a)` Tất cả các đường chéo xuất phát từ đỉnh `T` là: `TN;TP;TQ`
`b)` Ba cạnh kề nhau bất kì:
`@TM` và `MN`
`@RQ` và `QP`
`@NP` và `MN`
`c)` Tất cả các cạnh không kề với cạnh `PQ` là: `TR;TM;MN`
Đúng 1
Bình luận (0)
Bài 6. Các cạnh của hình chữ nhật tỉ lệ với 4 và 5. Tính các cạnh biết diện tích là 80cm vuông
Gọi độ dài các cạnh lần lượt là a,b
Theo đề, ta có: a/4=b/5 và ab=80
a/4=b/5=k
=>a=4k; b=5k
ab=80
=>20k^2=80
=>k=2
=>a=8; b=10
Đúng 2
Bình luận (0)
Bài 3:
a: Xét tứ giác ACDH cpó
F là trung điểm chung của AD và CH
nên ACDH là hình bình hành
b: ACDH là hình bình hành
nên DC//HA
=>DC vuông góc với BC
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A, biết AB=6cm, AC=8cm. Hạ AH vuông góc với BC. Qua H kẻ HE vuông tại AB, HF vuông tại AC
a) Tính BC và EF
b) Gọi M; N lần lượt là trung điểm của HB VÀ HC. Tính diện tích tứ giác MNFE
a) △ABC vuông tại A có:
\(BC^2=AB^2+AC^2\) (định lí Py-ta-go).
\(\Rightarrow BC^2=6^2+8^2=100\Rightarrow BC=10\left(cm\right)\)
\(AH.BC=AB.AC=2S_{ABC}\Rightarrow AH=\dfrac{AB.AC}{BC}=\dfrac{6.8}{10}=4,8\left(cm\right)\)
Tứ giác AEHF có: \(\widehat{EAF}=\widehat{AFH}=\widehat{AEH}=90^0\)
\(\Rightarrow\)AEHF là hình chữ nhật \(\Rightarrow AH=EF=4,8cm\).
b)\(S_{MNEF}=S_{MHE}+S_{NHF}+S_{HEF}=\dfrac{S_{BHE}}{2}+\dfrac{S_{HCF}}{2}+\dfrac{S_{AEHF}}{2}=\dfrac{S_{ABC}}{2}=\dfrac{AB.AC}{2}=\dfrac{6.8}{2}=24\left(cm^2\right)\)
Đúng 0
Bình luận (2)
Tính chiều cao của một lăng trụ đứng có chu vi đáy là 16cm và diện tích xung quanh bằng 128 cm2
bán kính đáy của đáy là:
16 : 3,14 : 2 = 2,5477707 (cm)
diện tích đáy là:
(2,5477707)2 x 3,14 = 20,38216559 (cm2)
chiều cao là:
128 : 20,38216559 = 6,28 (cm)
Đúng 4
Bình luận (0)
a: Xét ΔABD và ΔACE có
\(\widehat{ABD}=\widehat{ACE}\)
\(\widehat{BAD}=\widehat{CAE}\)
Do đó: ΔABD\(\sim\)ΔACE
b: \(\widehat{CED}=180^0-\widehat{ACE}-\widehat{CAE}\)
\(\widehat{CDE}=\widehat{ADB}=180^0-\widehat{ABD}-\widehat{BAD}\)
mà \(\widehat{CAE}=\widehat{BAD}\)
và \(\widehat{ACE}=\widehat{ABD}\)
nên \(\widehat{CED}=\widehat{CDE}\)
hay ΔCDE cân tại C
Đúng 2
Bình luận (0)
Cho Tam giác EDM nhọn .Gọi A,B,C lần lượt là trung điểm của ED,EM,MD
A,nhận dạng tứ giác ABMD
b,nhận dạng tứ giác ABCD
c,giả sử tam giác EDM cân tại E,nhận dạng tứ giác ABMD
d,giả sử tam giác EDM vuông tại D,nhận dạng tứ giác ABCD
e,Giả sử tam giác EDM vuông cân tại D,nhận dạng tứ giác ABCD
(Giúp với ạ tí mình thi rồi ạ)
a: Xét ΔEDM có
A là trung điểm của ED
B là trung điểm của EM
Do đó: AB là đường trung bình
=>AB//MD
hay ABMD là hình thang
b: Xét tứ giác ABCD có
AB//DC
AB=DC
Do đó: ABCD là hình bình hành
Đúng 1
Bình luận (0)
Hình học lớp 8
Cho tam giác ABC có 3 góc nhọn. Vẽ hai đường cao BD và CE (D thuộc AC, E thuộc AB)
a) Chứng minh: Tam giác ADB đồng dạng tam giác AEC
b) Chứng minh: AD. AC = AB.AE
c) Biết DE= 2cm, BC = 4cm. Tính diện tích ADE/ diện tích ABC
(Mai thi rồi cíu tôi đi 💦) 
a, Xét tam giác ADB và tam giác AEC có
^ADB = ^AEC = 900
^DAB _ chung
Vậy tam giác ADB ~ tam giác AEC (g.g)
b, \(\dfrac{AD}{AE}=\dfrac{AB}{AC}\Rightarrow AD.AC=AB.AE\)
c, \(\dfrac{S_{ADE}}{S_{ABC}}=\left(\dfrac{DE}{BC}\right)^2=\dfrac{1}{4}\)
Đúng 2
Bình luận (1)
Cho hình bình hành ABCD có góc B bằng lớn hơn 90 độ qua B kẻ đường thẳng vuông góc với AC tại O cắt AB tại E Chứng minh OA.OD = OC x OE
tứ giác ABCD có 2 đường chéo AC BD vuông góc với nhau. Gọi E;F;G;H lần lượt là trung điểm AB;BC;CD;AD.a) c/m tứ giác EFGH là hình chữ nhật.b) tính diện tích EFGH bt AC=8 cm;BD =6cm