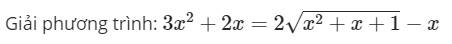Chương 3: PHƯƠNG TRÌNH, HỆ PHƯƠNG TRÌNH

2*sin x=2m+3

=>sin x=m+3/2

\(x\in\left[0;pi\right]\)

=>sin x thuộc [0;1]

=>0<=m+3/2<=1

=>-3/2<=m<=-1/2

ĐKXĐ: `x\inRR`

`pt<=>3(x^2+x)=2sqrt(x^2+x+1)`

Đặt `x^2+x=t(\text(Nhận xét: 't>=-0,25 \text( do ) x^2+x>=-0,25)`

`pt` trở thành `3t=2sqrt(t+1)`

`=>9t^2=4(t+1)`

`<=>9t^2-4t-4=0`

`\Delta '=(-2)^2-9.(-4)=40>0`

`=>t=(2+sqrt40)/9(TM)` hoặc `t=(2-sqrt40)/9(L)`

Suy ra `x^2+x=(2+sqrt40)/9`

`<=>(x+1/2)^2=(13+4\sqrt10)/18`

`=>x=+-sqrt((13+4\sqrt10)/18)-1/2`

Vậy `S={+-sqrt((13+4\sqrt10)/18)-1/2}`

bạn coi lại đề đúng chưa chứ giải nó lạ lắm

Ủa đề đúng mà tarrr?

Đặt \(t=\sqrt{x^2+x+1}\) 

PT: \(3x^2+2x=2\sqrt{x^2+x+1}-x\) \(\Leftrightarrow3x^2+3x+3-3=2\sqrt{x^2+x+1}\) 

\(\Leftrightarrow3\left(x^2+x+1\right)-3=2\sqrt{x^2+x+1}\) \(\Rightarrow3t^2-2t-3=0\)

Từ đó là ra thôi mà :)))

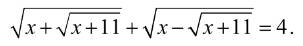
ĐKXĐ : \(\left\{{}\begin{matrix}x\ge-11\\x\ge\sqrt{x+11}\\x\ge-\sqrt{x+11}\end{matrix}\right.\)

Phương trình đã cho tương đương : 

\(x+\sqrt{x+11}+x-\sqrt{x+11}+2\sqrt{\left(x-\sqrt{x+11}\right).\left(x+\sqrt{x+11}\right)=16}\)

\(\Leftrightarrow x+\sqrt{x^2-x-11}=8\)

\(\Leftrightarrow\left\{{}\begin{matrix}x^2-x-11=\left(8-x\right)^2\\x\le8\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}15x=75\\x\le8\end{matrix}\right.\Leftrightarrow x=5\) (tm)

=>\(\dfrac{x^2-3x+6-x^2+3x-6}{\sqrt{x^2-3x+6}-\sqrt{x^2-3x+3}}=3\)

=>căn x^2-3x+6-căn x^2-3x+3=1

Đặt x^2-3x+3=a

=>căn a+3-căn a=1

=>a+3+a-2căn a^2+3a=1

=>2*căn (a^2+3a)=2a+3-1=2a+2

=>căn a^2+3a=a+1

=>a^2+3a=a^2+2a+1

=>a=1

=>x^2-3x+2=0

=>x=1 hoặc x=2

4:

A giao B=rỗng

=>4a<16/a

=>4a^2-16/a<0

=>4a^2-16>0

=>a>4 hoặc a<-4

=>a<-4

Số cách xếp 24 học sinh là 24!

Khi cho 4 bạn có tên trong đề ngồi cạnh nhau thì có 4! cách xếp

Có 4 hàng dọc, mà mỗi hàng dọc thì có 3 th là 1-2-3-4; 2-3-4-5; 3-4-5-6

=>Có 3*4*4!*20!

=>P=2/1771

x+my=m+1 và mx+y=3m-1

=>y=3m-1-mx và x+m(3m-1-mx)=m+1 và y=3m-1-mx

=>x+3m^2-m-m^2x=m+1 và y=3m-1-mx

=>x(1-m^2)=m+1-3m^2+m và y=3m-1-mx

=>x(m^2-1)=3m^2-2m-1 và y=3m-1-mx

=>x(m-1)(m+1)=(m-1)(3m+1) và y=3m-1-mx

Khi m=1 thì hệ vô số nghiệm

Khi m=-1 thì hệ vô nghiệm

Khi m<>1; m<>-1 thì hệ sẽ có nghiệm duy nhất là:

\(\left\{{}\begin{matrix}x=\dfrac{3m+1}{m+1}\\y=3m-1-\dfrac{3m^2+m}{m+1}=\dfrac{3m^2+3m-m-1-3m^2-m}{m+1}=\dfrac{m-1}{m+1}\end{matrix}\right.\)

x^2-y^2=4

=>\(\dfrac{9m^2+6m+1-m^2+2m-1}{m^2+2m+1}=4\)

=>\(8m^2+8m=4m^2+8m+4\)

=>4m^2=4

=>m=1(loại); m=-1(loại)

=>Ko có m

a: BC: x+y+4=0

=>AH: -x+y+c=0

Thay x=-1 và y=-2 vào AH, ta được:

c+1-2=0

=>c=1

=>-x+y+1=0

=>x-y-1=0

b: BC: x+y+4=0

=>B(x;-x-4)

Tọa độ M là:

xM=(x-1)/2 và yM=(-x-4-2)/2=(-x-6)/2

BC: x+y+4=0

=>MN: x+y+c=0

Thay xM=(x-1)/2 và yM=(-x-6)/2 vào MN, ta được:

\(\dfrac{x-1}{2}+\dfrac{-x-6}{2}+c=0\)

=>c+(1/2x-1/2-1/2x-3)=0

=>c=7/2

=>x+y+7/2=0