Question

Cho hình chóp S.ABCD có đáy là hình vuông cạnh đáy bằng 2a, các cạnh bên đều bằng \(a\sqrt{5}\). Góc giữa SA và mặt phẳng (SCD)

Answer 1

Answer 2

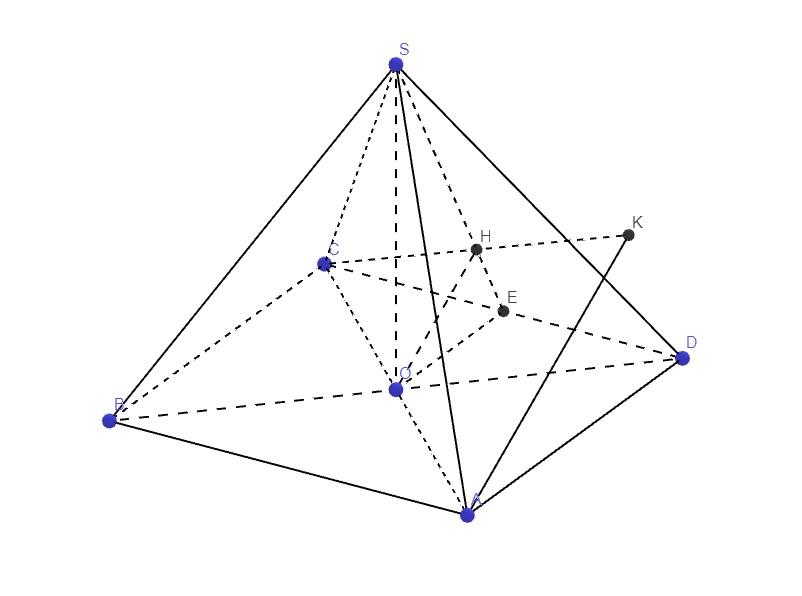
Gọi E là trung điểm CD \(\Rightarrow CD\perp\left(SOE\right)\)

Kẻ \(OH\perp SE\Rightarrow OH\perp\left(SCD\right)\)

Qua A kẻ đường thẳng song song OH, cắt CH kéo dài tại K

\(\Rightarrow AK\perp\left(SCD\right)\Rightarrow\widehat{ASK}\) là góc giữa SA và (SCD)

\(SO=\sqrt{SA^2-OA^2}=a\sqrt{3}\)

\(OH=\dfrac{SO.OE}{\sqrt{SO^2+OE^2}}=\dfrac{a\sqrt{3}}{2}\)

\(AK=2OH=a\sqrt{3}\) (đường trung bình)

\(sin\widehat{ASK}=\dfrac{AK}{SA}=\dfrac{\sqrt{15}}{5}\)