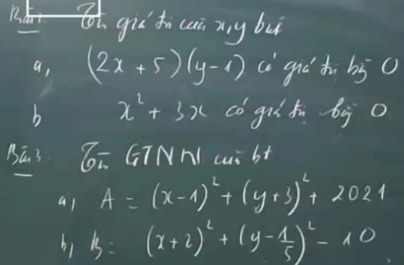Bài 4: Đơn thức đồng dạng
1/2 xy^2-1/3 y^2-(-2/5 xy^2)+2/5y^3
\(\dfrac{1}{2}xy^2-\dfrac{1}{3}y^2+\dfrac{2}{5}xy^2+\dfrac{2}{5}y^3=\dfrac{9}{10}xy^2-\dfrac{1}{3}y^2+\dfrac{2}{5}y^3\)
Đúng 0
Bình luận (0)
4x^3-2x^2+x^3-5x^2-x
\(4x^3-2x^2+x^3-5x^2-x=\left(4x^3+x^3\right)+\left(-2x^2-5x^2\right)-x=5x^3+\left(-7x^2\right)-x\)
Đúng 3
Bình luận (21)
Giúp mình bài 4,5,6 với ạ. Cảm ơn mọi người trước 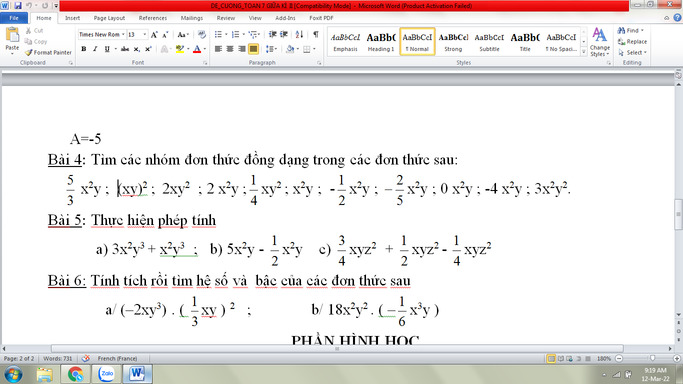
Bài 5:
a: \(=4x^2y^3\)
b: \(=\dfrac{9}{2}x^2y\)
c: \(=xyz^2\left(\dfrac{3}{4}-\dfrac{1}{4}+\dfrac{1}{2}\right)=xyz^2\)
Đúng 0
Bình luận (0)
Bài 4
Nhóm 1: \(\dfrac{5}{3}x^2y,2x^2y,x^2y,\dfrac{1}{2}x^2y,\dfrac{-1}{2}x^2y,\dfrac{-2}{5}x^2y,0x^2y,-4x^2y\)
Nhóm 2: \(\left(xy\right)^2,3x^2y^2\)
Bài 5
\(a,3x^2y^3+x^2y^3\)
\(=4x^2y^3\)
\(b,5x^2y-\dfrac{1}{2}x^2y\)
\(=\left(5-\dfrac{1}{2}\right)\left(x^2y\right)\)
\(=\dfrac{9}{2}x^2y\)
\(c,\dfrac{3}{4}xyz^2+\dfrac{1}{2}xyz^2-\dfrac{1}{4}xyz^2\)
\(=\left(\dfrac{3}{4}+\dfrac{1}{2}-\dfrac{1}{4}\right)\left(xyz^2\right)\)
\(=\left(\dfrac{3}{4}+\dfrac{2}{4}-\dfrac{1}{4}\right)\left(xyz^2\right)\)
\(=xyz^2\)
Bài 6
\(a,\left(-2xy^3\right)\left(\dfrac{1}{3}xy\right)^2\)
\(=\left(-2.\dfrac{1}{9}\right)\left(x.x^2\right)\left(y^3y^2\right)\)
\(=\dfrac{-2}{9}x^3y^5\)
Bậc: 3 + 5 = 8
Hệ số: \(\dfrac{-2}{9}\)
\(b,18x^2y^2\left(\dfrac{-1}{6}x^3y\right)\)
\(=\left(-18.\dfrac{1}{6}a\right)\left(x^2x^2\right)\left(y^2y^3\right)\)
\(=-3ax^4y^5\)
Bậc: 4 + 5 = 9
Hệ số: \(-3a\)
Đúng 0
Bình luận (0)
Đề bài: Cho các đơn thức A= -2/3 xymũ2 z ; B= -1/5 xz mũ3
a) Hãy chỉ ra phần hệ số, phần biến và tìm bậc của các đơn thức A; B.
b) Tìm đơn thức C biết C = A.B .
c) Tính giá trị của đơn thức A, B khi x = - 1; y = 2; z = -3.
d) Chứng minh rằng đơn thức C > 0 với mọi x; y ; z khác 0.
giúp mình vs mình đang cần gấp cảm ơn!
Đơn thức đồng dạng với đơn thức 3xy2 là:
A. 3xy B. -1/.x2y C. 3xy2 + 1 D. xy2
Xem thêm câu trả lời
Cho M = \(\dfrac{3x+9}{x+2}\)
a. Tìm x để M có nghĩa
b.Tìm x để M = 4
c. Tìm x ∈ Z để M ∈ Z.
a: Để M có nghĩa thì x+2<>0
hay x<>-2
b: Để M=4 thì 4x+8=3x+9
hay x=1(nhận)
c: Để M là số nguyên thì \(3x+9⋮x+2\)
\(\Leftrightarrow3x+6+3⋮x+2\)
\(\Leftrightarrow x+2\in\left\{1;-1;3;-3\right\}\)
hay \(x\in\left\{-1;-3;1;-5\right\}\)
Đúng 2
Bình luận (0)
`a)`
Để `M` có nghĩa thì:
`x+2\ne0`
`<=>x\ne-2`
Vậy `x\ne-2` thì `M` có nghĩa
`b)`
`M=4`
`<=>(3x+9)/(x+2)=4`
`=>4x+8=3x+9`
`<=>4x-3x=9-8`
`<=>x=1`
Vậy `x=1` thì `M=4`
`c)`
`M\inZZ<=>(3x+9)/(x+2)\inZZ`
`=>3x+9\vdotsx+2`
`=>3x+6+3\vdotsx+2`
`=>3.(x+2)+3\vdotsx+2`
`=>x+2\in Ư(3)={+-1;+-3}`
Ta có bảng:
$\begin{array}{|c|c|}\hline x+2&1&-1&3&-3\\\hline x&-1&-3&1&-5\\\hline\end{array}$
Vậy `x\in{-1;-3;1;-5}` thì `M\inZZ`
Đúng 1
Bình luận (0)
a) Để M có nghĩa thì x+2<>0
hay x<>-2
b) Để M=4 thì 4x+8=3x+9
hay x=1(nhận)
c) Để M là số nguyên thì 3x+9⋮x+23x+9⋮x+2
⇔3x+6+3⋮x+2⇔3x+6+3⋮x+2
⇔x+2∈{1;−1;3;−3}⇔x+2∈{1;−1;3;−3}
hay x∈{−1;−3;1;−5}
Đúng 0
Bình luận (0)
Bài 3:
a: \(A=\left(x-1\right)^2+\left(y+3\right)^2+2021\ge2021\forall x,y\)
Dấu '=' xảy ra khi x=1 và y=-3
b: \(B=\left(x+2\right)^2+\left(y-\dfrac{1}{5}\right)^2-10\ge-10\forall x,y\)
Dấu '=' xảy ra khi x=-2 và y=1/5
Đúng 0
Bình luận (0)
Bài 1:
\(a,\left(2x+5\right)\left(y-1\right)=0\\
\Leftrightarrow\left[{}\begin{matrix}2x+5=0\\y-1=0\end{matrix}\right.\\
\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5}{2}\\y=1\end{matrix}\right.\\
n,x^2+3x=0\\
\Leftrightarrow x\left(x+3\right)=0\\
\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-3\end{matrix}\right.\)
Bài 2:
a, Ta có:\(A=\left(x-1\right)^2+\left(y+3\right)^2+2021\ge2021\)
Dấu "=" xảy ra \(\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-3\end{matrix}\right.\)
Vậy \(A_{min}=2021\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-3\end{matrix}\right.\)
b, Ta có: \(B=\left(x+2\right)^2+\left(y-\dfrac{1}{5}\right)^2-10\ge-10\)
Dấu "=" xảy ra \(\Leftrightarrow\left\{{}\begin{matrix}x=-2\\y=\dfrac{1}{5}\end{matrix}\right.\)Vậy \(B_{min}=-10\Leftrightarrow\left\{{}\begin{matrix}x=-2\\y=\dfrac{1}{5}\end{matrix}\right.\)
Đúng 0
Bình luận (2)
Chứng tỏ (-3x)\(xy^2\)+\(^{ }\left(-2xy\right)^2\) luôn nhận giá trị ko âm vs mọi giá trị x,y
mk đg cần gấp á giúp nha
\(\left(-3x\right)\cdot xy^2+\left(-2xy\right)^2=-3x^2y^2+4x^2y^2=x^2y^2>=0\forall x,y\)
Đúng 1
Bình luận (0)