Chào mọi người, em đang bí câu này, mong được sự giúp đỡ gợi ý từ thầy cô và các bạn ạ, em cảm ơn. <3
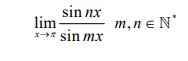
Chào mọi người, em đang bí câu này, mong được sự giúp đỡ gợi ý từ thầy cô và các bạn ạ, em cảm ơn. <3
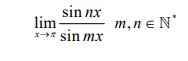
Tìm \(lim\left(\sqrt{4n^2+n}-\sqrt{4n^2+2}\right)\)
\(lim\left(\sqrt{4n^2+n}-\sqrt{4n^2+2}\right)\)
\(=lim\dfrac{\left(\sqrt{4n^2+n}-\sqrt{4n^2+2}\right)\times\left(\sqrt{4n^2+n}+\sqrt{4n^2+2}\right)}{\left(\sqrt{4n^2+n}+\sqrt{4n^2+2}\right)}\)
\(=lim\dfrac{\left(\sqrt{4n^2+n}\right)^2-\left(\sqrt{4n^2+2}\right)^2}{\sqrt{4n^2+n}+\sqrt{4n^2+2}}\)
\(=lim\dfrac{4n^2+n-4n^2-2}{\sqrt{4n^2+n}+\sqrt{4n^2+2}}\)
\(=lim\dfrac{n-2}{\sqrt{4n^2+n}+\sqrt{4n^2+2}}\)
\(=lim\dfrac{\dfrac{n}{n}-\dfrac{2}{n}}{\dfrac{n}{n}\sqrt{\dfrac{4n^2}{n^2}+\dfrac{n}{n^2}}+\dfrac{n}{n}\sqrt{\dfrac{4n^2}{n^2}+\dfrac{2}{n^2}}}\)
\(=\dfrac{1-0}{1\sqrt{4+0}+1\sqrt{4+0}}\)
\(=\dfrac{1}{2+2}\)
\(=\dfrac{1}{4}\)
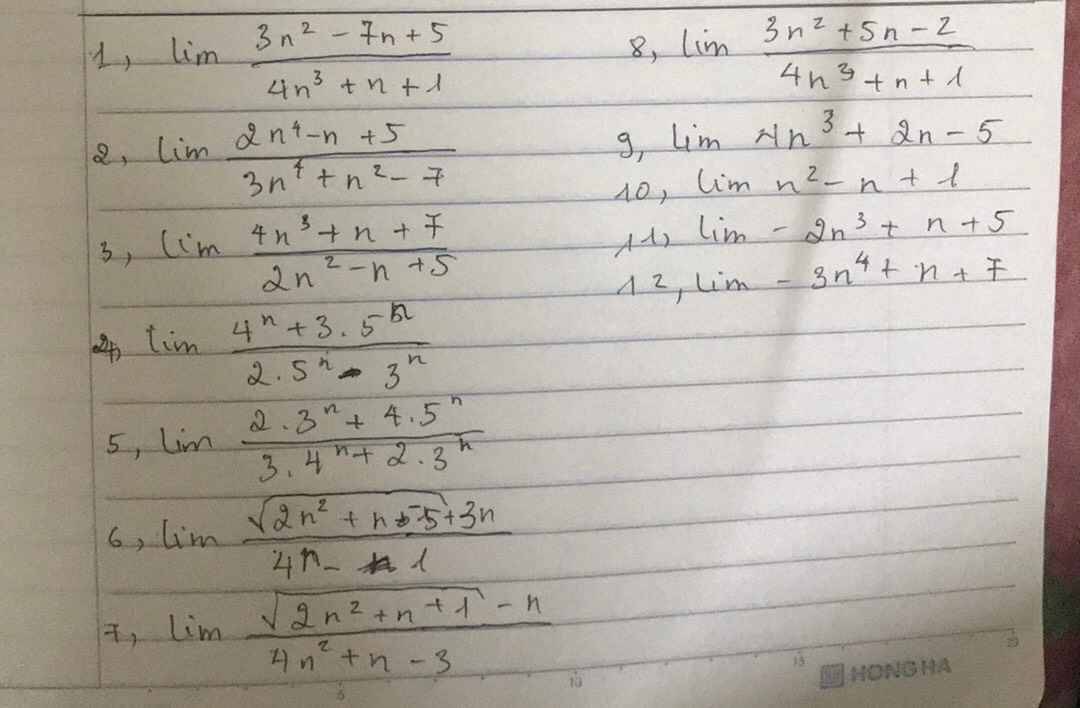
(mình đang cần gấp ạ!!)
1: \(=lim\left(\dfrac{\dfrac{3}{n}-\dfrac{7}{n^2}+\dfrac{5}{n^3}}{4+\dfrac{1}{n^2}+\dfrac{1}{n^3}}\right)=0\)
2: \(=lim\left(\dfrac{2-\dfrac{1}{n^3}+\dfrac{5}{n^4}}{3+\dfrac{1}{n^2}-\dfrac{7}{n^4}}\right)=\dfrac{2}{3}\)
3: \(=lim\left(\dfrac{4+\dfrac{1}{n^2}+\dfrac{7}{n^3}}{\dfrac{2}{n}-\dfrac{1}{n^2}+\dfrac{5}{n^3}}\right)=+\infty\)
4: \(=lim\left(\dfrac{\left(\dfrac{4}{5}\right)^n+3}{2-\left(\dfrac{3}{5}\right)^n}\right)=\dfrac{3}{2}\)
5: \(=lim\left(\dfrac{2\cdot\left(\dfrac{3}{5}\right)^n+4}{3\cdot\left(\dfrac{4}{5}\right)^n+2\cdot\left(\dfrac{3}{5}\right)^n}\right)=+\infty\)
6: \(=lim\left(\dfrac{\sqrt{2+\dfrac{1}{n}-\dfrac{5}{n^2}}+3}{4-\dfrac{1}{n}}\right)=\dfrac{3}{4}\)
7: \(=lim\left(\dfrac{\sqrt{\dfrac{2}{n^2}+\dfrac{1}{n^3}+\dfrac{1}{n^4}}-\dfrac{1}{n}}{4+\dfrac{1}{n}-\dfrac{3}{n^2}}\right)=+\infty\)
\(8,lim\dfrac{3n^2+n-2}{4n^3+n+1}\)
\(=lim\dfrac{\dfrac{3n^2}{n^3}+\dfrac{n}{n^3}-\dfrac{2}{n^3}}{\dfrac{4n^3}{n^3}+\dfrac{n}{n^3}+\dfrac{1}{n^3}}\)
\(=lim\dfrac{\dfrac{3}{n}+\dfrac{1}{n^2}-\dfrac{2}{n^3}}{4+\dfrac{1}{n^2}+\dfrac{1}{n^3}}\)
\(=\dfrac{0}{4}\)
\(=0\)
\(9,lim4n^3+2n-5\)
\(=lim\left(\dfrac{4n^3}{n^3}+\dfrac{2n}{n^3}-\dfrac{5}{n^3}\right)\)
\(=lim\left(4+\dfrac{2}{n^2}-\dfrac{5}{n^3}\right)\)
\(=4\)
\(10,lim\left(n^2-n+1\right)\)
\(=lim\left(\dfrac{n^2}{n^2}-\dfrac{n}{n^2}+\dfrac{1}{n^2}\right)\)
\(=lim\left(1-\dfrac{1}{n}+\dfrac{1}{n^2}\right)\)
\(=1\)
\(11,lim\left(-2n^3+n+5\right)\)
\(=lim\left(-\dfrac{2n^3}{n^3}+\dfrac{n}{n^3}+\dfrac{5}{n^3}\right)\)
\(=lim\left(-2+\dfrac{1}{n^2}+\dfrac{5}{n^3}\right)\)
\(=-2\)
\(12,lim\left(-3n^4+n+7\right)\)
\(=lim\left(-\dfrac{3n^4}{n^4}+\dfrac{n}{n^4}+\dfrac{7}{n^4}\right)\)
\(=lim\left(-3+\dfrac{1}{n^3}+\dfrac{7}{n^4}\right)\)
\(=-3\)
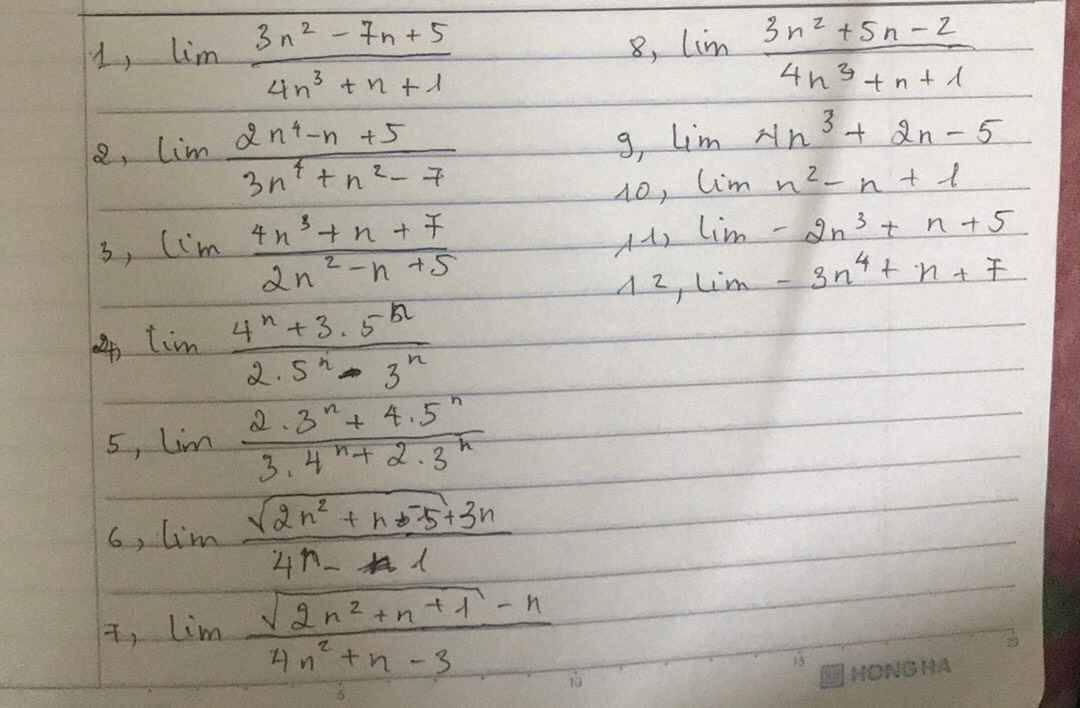
(mình đag cần gấp ạ ;'< !!!!)
1: \(=lim\left(\dfrac{\dfrac{3}{n}-\dfrac{7}{n^2}+\dfrac{5}{n^3}}{4+\dfrac{1}{n^2}+\dfrac{1}{n^3}}\right)=0\)
2: \(=lim\left(\dfrac{2-\dfrac{1}{n^3}+\dfrac{5}{n^4}}{3+\dfrac{1}{n^2}-\dfrac{7}{n^4}}\right)=\dfrac{2}{3}\)
3: \(=lim\left(\dfrac{4+\dfrac{1}{n^2}+\dfrac{7}{n^3}}{\dfrac{2}{n}-\dfrac{1}{n^2}+\dfrac{5}{n^3}}\right)=+\infty\)
4: \(=lim\left(\dfrac{\left(\dfrac{4}{5}\right)^n+3}{2-\left(\dfrac{3}{5}\right)^n}\right)=\dfrac{3}{2}\)
5: \(=lim\left(\dfrac{2\cdot\left(\dfrac{3}{5}\right)^n+4}{3\cdot\left(\dfrac{4}{5}\right)^n+2\cdot\left(\dfrac{3}{5}\right)^n}\right)=+\infty\)
6: \(=lim\left(\dfrac{\sqrt{2+\dfrac{1}{n}-\dfrac{5}{n^2}}+3}{4-\dfrac{1}{n}}\right)=\dfrac{3}{4}\)
7: \(=lim\left(\dfrac{\sqrt{\dfrac{2}{n^2}+\dfrac{1}{n^3}+\dfrac{1}{n^4}}-\dfrac{1}{n}}{4+\dfrac{1}{n}-\dfrac{3}{n^2}}\right)=+\infty\)
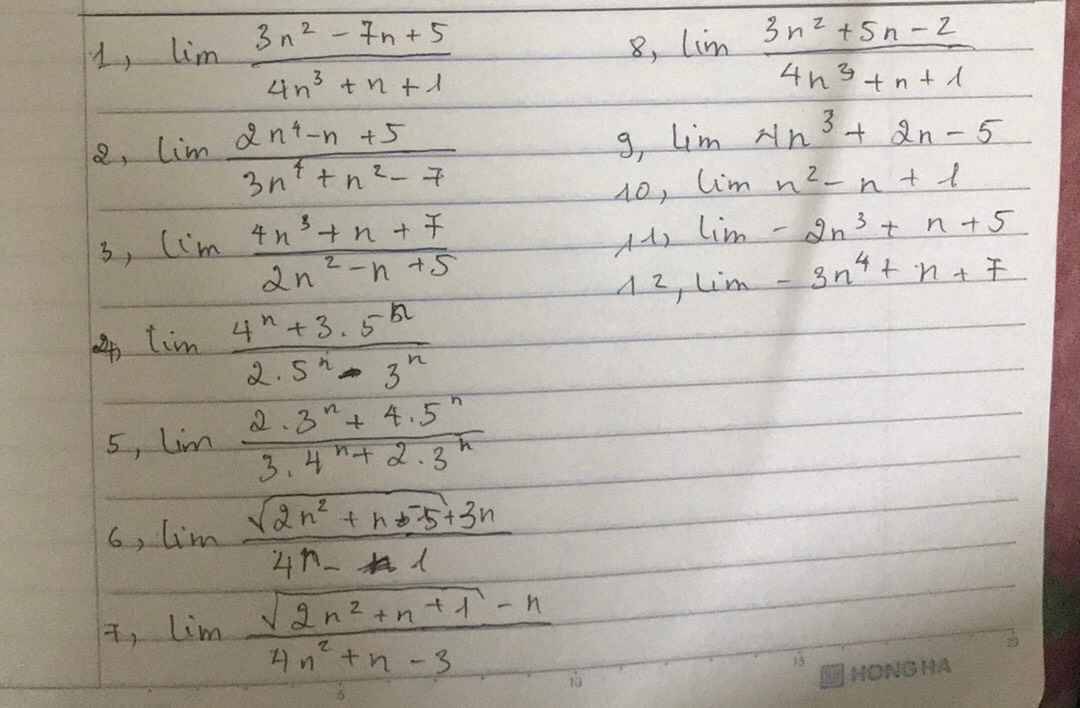
(mình đag cần gấp!)
Tính các giới hạn sau:
a) \(\lim\limits\dfrac{\sqrt[3]{n^6-7n^3-5n+8}}{n+12}\)
b) \(\lim\limits\dfrac{1}{\sqrt{3n+2}-\sqrt{2n+1}}\)
c) \(\lim\limits\dfrac{4.3^n+7^{n+1}}{2.5^n+7^n}\)
a.
\(A=\lim\frac{\sqrt[3]{n^6-7n^3-5n+8}}{n+12}=\lim \frac{\sqrt[3]{\frac{n^6-7n^3-5n+8}{n^3}}}{\frac{n+12}{n}}=\lim \frac{\sqrt[3]{n^3-7-\frac{5}{n^2}+\frac{8}{n^3}}}{1+\frac{12}{n}}\)
Ta thấy:
\(\lim\sqrt[3]{n^3-7-\frac{5}{n^2}+\frac{8}{n^3}}=\infty \)
\(\lim (1+\frac{12}{n})=1\)
Suy ra $A=\infty$
b.
\(B=\lim\frac{1}{\sqrt{3n+2}-\sqrt{2n+1}}=\lim \frac{1}{\frac{3n+2-(2n+1)}{\sqrt{3n+2}+\sqrt{2n+1}}}=\lim \frac{\sqrt{3n+2}+\sqrt{2n+1}}{n+1}\)
\(=\lim \frac{\sqrt{\frac{3n+2}{n}}+\sqrt{\frac{2n+1}{n}}}{\frac{n+1}{\sqrt{n}}}=\lim \frac{\sqrt{3+\frac{2}{n}}+\sqrt{2+\frac{1}{n}}}{\sqrt{n}+\frac{1}{\sqrt{n}}}\)
Ta thấy:
\(\lim( \sqrt{3+\frac{2}{n}}+\sqrt{2+\frac{1}{n}})=\sqrt{3}+\sqrt{2}>0\)
\(\lim (\sqrt{n}+\frac{1}{\sqrt{n}})=\infty\)
$\Rightarrow B=\infty$
c.
\(C=\lim \frac{4.3^n+7^{n+1}}{2.5^n+7^n}=\lim \frac{4(\frac{3}{7})^n+7}{2(\frac{5}{7})^n+1}\)
Ta thấy:
\(\lim [4(\frac{3}{7})^n+7]=4.0+7=7\) với $|\frac{3}{7}|<1$
\(\lim [2(\frac{5}{7})^n+1]=2.0+1=1\) với $|\frac{5}{7}|<1$
$\Rightarrow C=\frac{7}{1}=7$
execute at @e[type=snowball] run summon tnt
\(5,lim\left(\sqrt{n^2+n}-\sqrt{n^2+2}\right)\)
\(=lim\dfrac{\left(\sqrt{n^2+n}\right)^2-\left(\sqrt{n^2+2}\right)^2}{\left(\sqrt{n^2+n}\right)+\left(\sqrt{n^2+2}\right)^2}\)
\(=lim\dfrac{n^2+n-n^2-2}{\left(\sqrt{n^2+n}\right)+\left(\sqrt{n^2+2}\right)}\)
\(=lim\dfrac{n-2}{\left(\sqrt{n^2+n}\right)+\left(\sqrt{n^2+2}\right)}\)
\(=lim\dfrac{\dfrac{n}{n}-\dfrac{2}{n}}{\left(\dfrac{\sqrt{n^2}}{n^2}+\dfrac{\sqrt{n}}{n^2}\right)+\left(\dfrac{\sqrt{n^2}}{n^2}+\dfrac{2}{n^2}\right)}\)
\(=\dfrac{1-0}{1+0+1+0}\)
\(=\dfrac{1}{2}\)
\(7,lim\left(n+1-\sqrt{n^2+2n+5}\right)\)
\(=lim\left(n-\sqrt{n^2+2n+5}+1\right)\)
\(=lim\dfrac{\left(n-\sqrt{n^2+2n+5}\right)\left(n+\sqrt{n^2+2n+5}\right)}{n+\sqrt{n^2+2n+5}}+1\)
\(=lim\dfrac{n^2-n^2+2n+5}{n+\sqrt{n^2+2n+5}}+1\)
\(=lim\dfrac{2n+5}{n+\sqrt{n^2+2n+5}}+1\)
\(=lim\dfrac{\dfrac{2n}{n}+\dfrac{5}{n}}{\dfrac{n}{n}+\sqrt{\dfrac{n^2}{n^2}+\dfrac{2n}{n^2}+\dfrac{5}{n^2}}}+1\)
\(=lim\dfrac{2+\dfrac{5}{n}}{1+\sqrt{1+\dfrac{2}{n}+\dfrac{5}{n^2}}}+1\)
\(=\dfrac{2+0}{1+\sqrt{1+0+0}}+1\)
\(=\dfrac{2}{2}+1\)
\(=1+1\)
\(=2\)
Tính các giới hạn sau:
a) \(\lim\limits\dfrac{2n^2+5}{-3n^2-3}\)
b) \(lim\left(-5n^3-2n^2+5n-6\right)\)
`a)lim[2n^2+5]/[-3n^2-3]`
`=lim[2+5/[n^2]]/[-3-3/[n^2]]`
`=2/[-3]=-2/3`
`b)lim(-5n^3-2n^2+5n-6)`
`=lim n^3(-5-2/n+5/[n^2]-6/[n^3])`
Vì `{:(lim n^3=+oo),(lim (-5-2/n+5/[n^2]-6/[n^3])=-5):}}=>lim n^3(-5-2/n+5/[n^2]-6/[n^3])=-oo`
Tính các giới hạn sau:
a) \(\lim\limits\dfrac{5n^3-3n^2+1}{1-3n^3}\)
b) \(\lim\limits\dfrac{-9n+5}{3n-3}\)
`a)lim[5n^3-3n^2+1]/[1-3n^3]`
`=lim[5-3/n+1/[n^3]]/[1/[n^3]-3]`
`=5/[-3]=-5/3`
_____________________________
`b)lim[-9n+5]/[3n-3]`
`=lim[-9+5/n]/[3-3/n]`
`=[-9]/3=-3`