Có cung \(\alpha\) nào mà \(\sin\alpha\) nhận các giá trị tương ứng sau đây không ?
a) \(-0,7\)
b) \(\dfrac{4}{3}\)
c) \(-\sqrt{2}\)
d) \(\dfrac{\sqrt{5}}{2}\)
Có cung \(\alpha\) nào mà \(\sin\alpha\) nhận các giá trị tương ứng sau đây không ?
a) \(-0,7\)
b) \(\dfrac{4}{3}\)
c) \(-\sqrt{2}\)
d) \(\dfrac{\sqrt{5}}{2}\)
Các đẳng thức sau có thể đồng thời xảy ra không ?
a) \(\sin\alpha=\dfrac{\sqrt{2}}{3}\) và \(\cos\alpha=\dfrac{\sqrt{3}}{3}\)
b) \(\sin\alpha=\dfrac{-4}{5}\) và \(\cos\alpha=-\dfrac{3}{5}\)
c) \(\sin\alpha=0,7\) và \(\cos\alpha=0,3\)
a) Không. Bởi vì
< 1
b) Có thể đồng thời xảy ra, vì = 1
c) Không. Lí do như câu a
Cho \(0< \alpha< \dfrac{\pi}{2}\). Xác định dấu của các giá trị lượng giác
a) \(\sin\left(\alpha-\pi\right)\)
b) \(\cos\left(\dfrac{3\pi}{2}-\alpha\right)\)
c) \(\tan\left(\alpha+\pi\right)\)
d) \(\cot\left(\alpha+\dfrac{\pi}{2}\right)\)
Với 0 < α < :
a) sin(α - π) < 0; b) cos( - α) < 0;
c) tan(α + π) > 0; d) cot(α + ) < 0
Tính các giá trị lượng giác của góc\(\alpha\), nếu :
a) \(\cos\alpha=\dfrac{4}{13}\) và \(0< \alpha< \dfrac{\pi}{2}\)
b) \(\sin\alpha=-0,7\) và \(\pi< \alpha< \dfrac{3\pi}{2}\)
c) \(\tan\alpha=-\dfrac{15}{7}\) và \(\dfrac{\pi}{2}< \alpha< \pi\)
d) \(\cot\alpha=-3\) và \(\dfrac{3\pi}{2}< \alpha< 2\pi\)
a) Do 0 < α < nên sinα > 0, tanα > 0, cotα > 0
sinα =
cotα = ; tanα =
b) π < α < nên sinα < 0, cosα < 0, tanα > 0, cotα > 0
cosα = -√(1 - sin2 α) = -√(1 - 0,49) = -√0,51 ≈ -0,7141
tanα ≈ 0,9802; cotα ≈ 1,0202.
c) < α < π nên sinα > 0, cosα < 0, tanα < 0, cotα < 0
cosα = ≈ -0,4229.
sinα =
cotα = -
d) Vì < α < 2π nên sinα < 0, cosα > 0, tanα < 0, cotα < 0
Ta có: tanα =
cosα =
Trả lời bởi Nguyễn Đắc Định
Cho \(\pi< \alpha< \dfrac{3\pi}{2}\). Xác định dấu của các giá trị lượng giác sau :
a) \(\cos\left(\alpha-\dfrac{\pi}{2}\right)\)
b) \(\sin\left(\dfrac{\pi}{2}+\alpha\right)\)
c) \(\tan\left(\dfrac{3\pi}{2}-\alpha\right)\)
d) \(\cot\left(\alpha+\pi\right)\)
Do \(\pi< \alpha< \dfrac{3\pi}{2}\) nên \(sin\alpha,cos\alpha< 0;tan\alpha,cot\alpha< 0\).
\(cos\left(\alpha-\dfrac{\pi}{2}\right)=cos\left(\dfrac{\pi}{2}-\alpha\right)=sin\alpha< 0\).
\(sin\left(\dfrac{\pi}{2}+\alpha\right)=cos\alpha< 0\).
\(tan\left(\dfrac{3\pi}{2}-\alpha\right)=tan\left(\dfrac{3\pi}{2}-\alpha-2\pi\right)\)\(=tan\left(-\dfrac{\pi}{2}-\alpha\right)\)\(=-tan\left(\dfrac{\pi}{2}+\alpha\right)=cot\left(\alpha\right)>0\).
\(cot\left(\alpha+\pi\right)=cot\left(\alpha\right)>0\).
Chứng minh rằng với mọi \(\alpha\), ta luôn có :
a) \(\sin\left(\alpha+\dfrac{\pi}{2}\right)=\cos\alpha\)
b) \(\cos\left(\alpha+\dfrac{\pi}{2}\right)=-\sin\alpha\)
c) \(\tan\left(\alpha+\dfrac{\pi}{2}\right)=-\cot\alpha\)
d) \(\cot\left(\alpha+\dfrac{\pi}{2}\right)=-\tan\alpha\)
a)\(sin\left(\alpha+\dfrac{\pi}{2}\right)=cos\left[\dfrac{\pi}{2}-\left(\alpha+\dfrac{\pi}{2}\right)\right]=cos\left(-\alpha\right)=cos\alpha\).
b) \(cos\left(x+\dfrac{\pi}{2}\right)=sin\left[\dfrac{\pi}{2}-\left(x+\dfrac{\pi}{2}\right)\right]=sin\left(-x\right)=-sinx\).
c) \(tan\left(\alpha+\dfrac{\pi}{2}\right)=\dfrac{sin\left(\alpha+\dfrac{\pi}{2}\right)}{cos\left(\alpha+\dfrac{\pi}{2}\right)}=\dfrac{cos\alpha}{-sin\alpha}=-cot\alpha\).
d) \(cot\left(\alpha+\dfrac{\pi}{2}\right)=\dfrac{cos\left(\alpha+\dfrac{\pi}{2}\right)}{sin\left(\alpha+\dfrac{\pi}{2}\right)}=\dfrac{-sin\alpha}{cos\alpha}=-tan\alpha\).
Tính các giá trị lượng giác của góc \(\alpha\), nếu :
a) \(\cos\alpha=-\dfrac{1}{4},\pi< \alpha< \dfrac{3\pi}{2}\)
b) \(\sin\alpha=\dfrac{2}{3},\dfrac{\pi}{2}< \alpha< \pi\)
c) \(\tan\alpha=\dfrac{7}{3},0< \alpha< \dfrac{\pi}{2}\)
d) \(\cot\alpha=-\dfrac{14}{9},\dfrac{3\pi}{2}< \alpha< 2\pi\)
a) Do \(\pi< \alpha< \dfrac{3\pi}{2}\) nên \(sin\alpha< 0;cot\alpha>0;tan\alpha>0\).
Vì vậy: \(sin\alpha=-\sqrt{1-cos^2\alpha}=\dfrac{-\sqrt{15}}{4}\).
\(tan\alpha=\dfrac{sin\alpha}{cos\alpha}=\dfrac{-\sqrt{15}}{4}:\dfrac{-1}{4}=\sqrt{15}\).
\(cot\alpha=\dfrac{1}{tan\alpha}=\dfrac{1}{\sqrt{15}}\).
Biết \(\sin\alpha=\dfrac{3}{4}\) và \(\dfrac{\pi}{2}< \alpha< \pi\). Tính :
a) \(A=\dfrac{2\tan\alpha-3\cot\alpha}{\cos\alpha+\tan\alpha}\)
b) \(B=\dfrac{\cos^2\alpha+\cot^2\alpha}{\tan\alpha-\cot\alpha}\)
Do \(\dfrac{\pi}{2}< \alpha< \pi\) nên \(tan\alpha< 0,cot\alpha< 0;cos\alpha< 0\).
Vì vậy: \(cos\alpha=-\sqrt{1-sin^2\alpha}=-\dfrac{\sqrt{7}}{4}\).
\(tan\alpha=\dfrac{sin\alpha}{cos\alpha}=\dfrac{3}{4}:\dfrac{-\sqrt{7}}{4}=\dfrac{-3}{\sqrt{7}}\).
\(cot\alpha=\dfrac{1}{tan\alpha}=\dfrac{-\sqrt{7}}{3}\).
\(A=\dfrac{2tan\alpha-3cot\alpha}{cos\alpha+tan\alpha}\)\(=\dfrac{2.\dfrac{-3}{\sqrt{7}}-3.\dfrac{-\sqrt{7}}{3}}{\dfrac{-\sqrt{7}}{4}+\dfrac{-3}{\sqrt{7}}}\)
\(=\dfrac{\dfrac{-6}{\sqrt{7}}+\sqrt{7}}{\dfrac{-7-12}{4\sqrt{7}}}\)\(=\dfrac{\dfrac{-6+7}{\sqrt{7}}.4\sqrt{7}}{-19}\)\(=\dfrac{\dfrac{1}{\sqrt{7}}.4\sqrt{7}}{-19}=-\dfrac{4}{19}\).
Cho \(\tan\alpha-3\cot\alpha=6\) và \(\pi< \alpha< \dfrac{3\pi}{2}\). Tính :
a) \(\sin\alpha+\cos\alpha\)
b) \(\dfrac{2\sin\alpha-\tan\alpha}{\cos\alpha+\cot\alpha}\)
a) Do \(\pi< \alpha< \dfrac{3\pi}{2}\) nên \(tan\alpha,cot\alpha>0\) và \(sin\alpha,cos\alpha< 0\).
\(\left\{{}\begin{matrix}tan\alpha-3cot\alpha=6\\tan\alpha cot\alpha=1\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}tan\alpha=6+3cot\alpha\\\left(6+3cot\alpha\right)cot\alpha=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}tan\alpha=6+3cot\alpha\\3cot^2\alpha+6cot\alpha-1=0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}tan\alpha=6+3cot\alpha\\cot\alpha=\dfrac{-3+2\sqrt{3}}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}tan\alpha=3+2\sqrt{3}\\cot\alpha=\dfrac{-3+2\sqrt{3}}{3}\end{matrix}\right.\).
Có \(1+tan^2\alpha=\dfrac{1}{cos^2\alpha}\Rightarrow cos^2\alpha=\dfrac{1}{tan^2\alpha+1}\).
Có thể đề sai.
Chứng minh các đẳng thức :
a) \(\dfrac{\tan\alpha-\tan\beta}{\cot\beta-\cot\alpha}=\tan\alpha\tan\beta\)
b) \(\tan100^0+\dfrac{\sin530^0}{1+\sin640^0}=\dfrac{1}{\sin10^0}\)
c) \(2\left(\sin^6\alpha+\cos^6\alpha\right)+1=3\left(\sin^4\alpha+\cos^4\alpha\right)\)
a) \(\dfrac{tan\alpha-tan\beta}{cot\beta-cot\alpha}=\dfrac{\dfrac{sin\alpha}{cos\alpha}-\dfrac{sin\beta}{cos\beta}}{\dfrac{cos\beta}{sin\beta}-\dfrac{cos\alpha}{sin\alpha}}\)
\(=\dfrac{\dfrac{sin\alpha cos\beta-cos\alpha sin\beta}{cos\alpha cos\beta}}{\dfrac{cos\beta sin\alpha-cos\alpha sin\beta}{sin\beta sin\alpha}}\)
\(=\dfrac{sin\beta sin\alpha}{cos\beta cos\alpha}=tan\alpha tan\beta\).
a) -1 ≤ -0,7 ≤ 1. Có cung α mà sin α = -0,7
b) > 1. Không có cung α có sin nhận giá trị
> 1. Không có cung α có sin nhận giá trị 
c) Không. Vì -√2 < -1
d) Không. Vì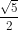 > 1
> 1
Trả lời bởi Nguyễn Đắc Định