Trong môn Bóng đá, độ khó của mỗi pha ghi bàn còn được tính bởi góc sút vào cầu môn là rộng hay hẹp. Nếu biết độ rộng của khung thành là 7,32 m, trái bóng cách hai cột gôn lần lượt là 10,98 m và 14,64 m thì em có cách nào để đo được góc sút ở vị trí này bởi các dụng cụ học tập không?
Bài 34. Ba trường hợp đồng dạng của hai tam giác
QL
Hướng dẫn giải
Thảo luận (1)
QL
Cho hai tam giác ABC và ABC có frac{{AB}}{{AB}} frac{{AC}}{{AC}} frac{{BC}}{{BC}}a) Nếu A′BAB thì hai tam giác có đồng dạng với nhau không? Vì sao?b) Nếu A′B- Hãy giải thích vì sao ΔAMN ∽ ΔABC- Hãy chứng tỏ rằng ANA’C’′, MNB′C′ để suy ra ΔAMN ΔABC (c.c.c)- Hai tam giác ABC và ABC có đồng dạng với nhau không? Nếu có, em hãy viết đúng kí hiệu đồng dạng giữa chúng.c) Nếu AB AB thì tam giác ABC có đồng dạng với tam giác ABC không? Vì sao?
Đọc tiếp
Cho hai tam giác ABC và A'B'C' có \(\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}} = \frac{{B'C'}}{{BC}}\)
a) Nếu A′B=AB thì hai tam giác có đồng dạng với nhau không? Vì sao?
b) Nếu A′B
- Hãy giải thích vì sao ΔAMN ∽ ΔABC
- Hãy chứng tỏ rằng AN=A’C’′, MN=B′C′ để suy ra ΔAMN = ΔA'B'C' (c.c.c)
- Hai tam giác A'B'C' và ABC có đồng dạng với nhau không? Nếu có, em hãy viết đúng kí hiệu đồng dạng giữa chúng.
c) Nếu A'B' > AB thì tam giác A'B'C' có đồng dạng với tam giác ABC không? Vì sao?

Hướng dẫn giải
Thảo luận (1)
a) Nếu A′B′=AB thì tam giác có đồng dạng.
Vì A′B′=AB \( \Rightarrow \)A’C’=AC => B’C’=BC => \(\widehat A = \widehat {A'};\widehat B = \widehat {B'};\widehat C = \widehat {C'}\)
=> Hai tam giác đồng dạng
b) MN // BC ( M∈AB, N∈AC) => ΔAMN ∽ ΔABC
=> \(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} = \frac{{MN}}{{BC}}\)
Mà \(\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}} = \frac{{B'C'}}{{BC}}\)
=> \(\frac{{A'B'}}{{AM}} = \frac{{A'C'}}{{AN}} = \frac{{B'C'}}{{MN}}\)
- Có AM= A’B’ => A’C’=AN \( \Rightarrow \) B’C’=MN
=> ΔAMN = ΔA'B'C'
=> ΔAMN ∽ ΔA'B'C'
Mà ΔAMN ∽ ΔABC
=> ΔABC ∽ ΔA′B′C′
c) Nếu A'B' > AB thì tam giác A'B'C' có đồng dạng với tam giác ABC. Vì \(\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}} = \frac{{B'C'}}{{BC}}\)
Trả lời bởi Hà Quang Minh
QL
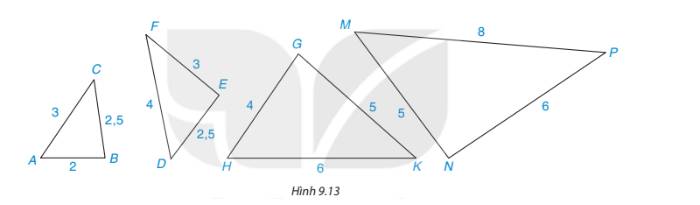
Những cặp tam giác nào dưới đây (hình 9.13) là đồng dạng? (các kích thước được tính theo đơn vị centimét). Viết đúng kí hiệu đồng dạng.
Hướng dẫn giải
Thảo luận (1)
Các cặp tam giác đồng dạng là: \(\Delta ABC \backsim \Delta HKG{;^{}}\Delta EFD \backsim \Delta NPM\)
Trả lời bởi Hà Quang Minh
QL
Cho tam giác ABC có chu vi bằng 18 cm và tam giác DEF có chu vi bằng 27cm. Biết rằng AB=4cm, BC=6cm, DE=6cm, FD=12cm. Chứng minh ΔABC ∽ ΔDEF
Hướng dẫn giải
Thảo luận (1)
Vì chu vi tam giác ABC bằng 18cm
=> AB+AC+BC=18 => 4+AC+6=18 => AC=8 (cm)
Vì chu vi tam giác DEF bằng 27cm
=> DE+EF+DF=27 => 6+EF+12=27 => EF=9 (cm)
Ta thấy \(\begin{array}{l}\frac{{AB}}{{DE}} = \frac{{AC}}{{DF}} = \frac{{BC}}{{EF}}\\ = \frac{4}{6} = \frac{8}{{12}} = \frac{6}{9} = \frac{2}{3}\end{array}\)
=> ΔABC ∽ ΔDEF
Trả lời bởi Hà Quang Minh
QL
Trở lại tình huống mở đầu. Em hãy vẽ một tam giác có ba cạnh tỉ lệ với ba cạnh của tam giác tạo bởi ba đỉnh là trái bóng và hai chân cột gôn. Từ đó tính góc sút bằng góc tương ứng của tam giác vừa vẽ được.
Vuông: Tớ sẽ tính tỉ lệ (7,32 : 10,98 : 14,64) bằng (1 : 1,5 : 2).
Tròn: Tớ sẽ tính tỉ lệ (7,32 : 10,98 : 14,64) bằng (2 : 3 : 4).
Hướng dẫn giải
Thảo luận (1)
Ta có tỉ lệ của độ rộng khung thành và khoảng cách hai cột gôn là: 7,32 : 10,98 : 14,64 = 2 : 3 : 4 nên độ dài cạnh của tam giác vẽ theo tỉ lệ 2 : 3 : 4.
Sử dụng thước đo góc, ta được \( \widehat C \approx 29^0 \) hay góc sút bằng khoảng \(29^0\).
Trả lời bởi Hà Quang Minh
QL
Cho hai tam giác ABC và A'B'C' có độ dài các cạnh (theo đơn vị cm) như Hình 9.15. Biết rằng \(\widehat A = \widehat {A'}\)

Hướng dẫn giải
Thảo luận (1)
- Có \(\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}} = \frac{2}{3}\)
- Có \(\frac{{B'C'}}{{BC}} = \frac{2}{3}\)
- Tam giác A'B'C' có đồng dạng với tam giác ABC và đồng dạng với tỉ số \(\frac{2}{3}\)
Trả lời bởi Hà Quang Minh
QL
Những cặp tam giác nào trong hình 9.17 là đồng dạng? (Các kích thước được tính theo đơn vị centimét). Viết đúng kí hiệu đồng dạng.
Hướng dẫn giải
Thảo luận (1)
Các cặp tam giác đồng dạng: \(\Delta ACB \backsim \Delta MPN\)
Trả lời bởi Hà Quang Minh
QL
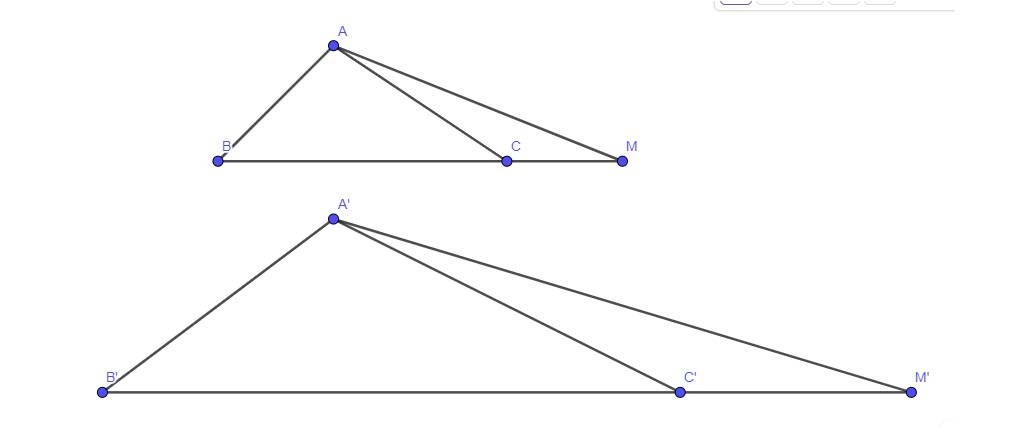
Cho ΔA'B'C' ∽ ΔABC. Trên tia đối của các tia CB, C'B' lần lượt lấy các điểm M, M' sao cho \(\frac{{MC}}{{MB}} = \frac{{M'C'}}{{M'B'}}\). Chứng minh rằng ΔA'B'M' ∽ ΔABM
Hướng dẫn giải
Thảo luận (1)
Ta có:
\(\begin{array}{l}\frac{{MC}}{{MB}} = \frac{{M'C'}}{{M'B'}}\\ \Rightarrow \frac{{MB - BC}}{{MB}} = \frac{{M'B' - B'C'}}{{M'B'}}\\ \Rightarrow 1 - \frac{{BC}}{{MB}} = 1 - \frac{{B'C'}}{{M'B'}}\\ \Rightarrow \frac{{BC}}{{MB}} = \frac{{B'C'}}{{M'B'}}\\ \Rightarrow \frac{{M'B'}}{{MB}} = \frac{{B'C'}}{{BC}}(1)\end{array}\)
Vì ΔA'B'C' ∽ ΔABC suy ra:
\(\begin{array}{l}\widehat {B'} = \widehat B\\\frac{{A'B'}}{{AB}} = \frac{{B'C'}}{{BC}}(2)\end{array}\)
Từ (1) và (2) suy ra:
\(\frac{{M'B'}}{{MB}} = \frac{{A'B'}}{{AB}}\)
Xét tam giác ABM và tam giác A”B”M’ có:
\(\begin{array}{l}\widehat {B'} = \widehat B\\\frac{{M'B'}}{{MB}} = \frac{{A'B'}}{{AB}}\end{array}\)
Suy ra \(\Delta A'B'M' \backsim \Delta ABM\)
Trả lời bởi Hà Quang Minh
QL
1. Bạn Lan nhận xét rằng nếu tam giác ABC và tam giác A’B’C’ có \(\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}}\) và \(\widehat {B'} = \widehat B\) thì chúng đồng dạng. Theo em bạn Lan nhận xét đúng không vì sao?
2. Nếu thêm giả thiết \(\widehat C\) và \(\widehat {C'}\) đều là góc nhọn thì tam giác ABC và A’B’C’ đồng dạng với nhau không?
Hướng dẫn giải
Thảo luận (1)
Khi góc ACB là góc tù, lấy điểm M trên tia BC sao cho tam giác AMC cân tại A nên AM = AC
Khi đó \(\Delta A'B'C' \backsim \Delta ABM\)
Như vậy nhận xét của Lan không chính xác.
Trả lời bởi Hà Quang Minh
QL
Bạn Tròn đang đứng ở vị trí điểm A bên bờ sông và nhờ anh Pi tính giúp khoảng cách từ chỗ mình đứng đến chân một cột cờ tại điểm C bên kia sông (H.9.20a). Anh Pi lấy một vị trí B sao cho AB10m, widehat {ABC} {70^o}{,^{}}widehat {BAC} {80^o} và vẽ một tam giác ABC trên giấy với A′B′2cm, widehat {ABC} {70^o};widehat {BAC} {80^o}(H.9.20b)Em hãy dự đoán xem tam giác ABC có đồng dạng với tam giác ABC không? nếu có thì tỉ số đồng dạng là bao nhiêu.
Đọc tiếp
Bạn Tròn đang đứng ở vị trí điểm A bên bờ sông và nhờ anh Pi tính giúp khoảng cách từ chỗ mình đứng đến chân một cột cờ tại điểm C bên kia sông (H.9.20a). Anh Pi lấy một vị trí B sao cho AB=10m, \(\widehat {ABC} = {70^o}{,^{}}\widehat {BAC} = {80^o}\) và vẽ một tam giác A'B'C' trên giấy với A′B′=2cm, \(\widehat {A'B'C'} = {70^o};\widehat {B'A'C'} = {80^o}\)(H.9.20b)
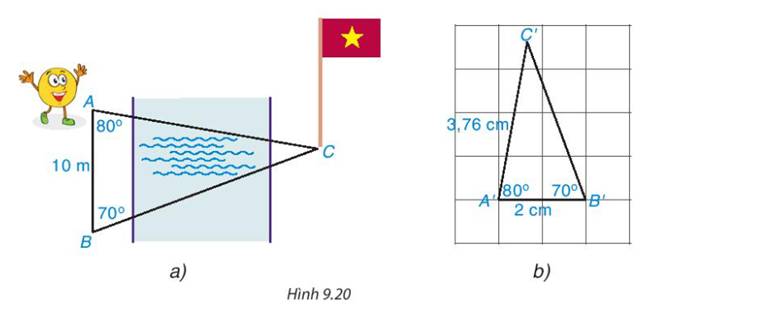
Em hãy dự đoán xem tam giác A'B'C' có đồng dạng với tam giác ABC không? nếu có thì tỉ số đồng dạng là bao nhiêu.
Hướng dẫn giải
Thảo luận (1)
Tam giác A'B'C' đồng dạng với tam giác ABC với tỉ số đồng dạng \(\frac{1}{5}\)
Trả lời bởi Hà Quang Minh
Vì trong hình vẽ mặt sân được vẽ nghiêng nên nếu đo trực tiếp trong sách giáo khoa sẽ không đúng bằng góc thực tế.
Vẽ một tam giác bằng dụng cụ học tập trên giấy có một góc đúng bằng góc sút. Từ đó sử dụng dụng cụ học tập là thước đo góc để đo góc sút.
Trả lời bởi Hà Quang Minh