Có một chiếc bóng điện được mắc trên đỉnh (Điểm A) của cột đèn thẳng đứng. Để tính chiều cao AB của cột đèn, bác Dương cắm một chiếc cọc gỗ (đoạn CD) thẳng đứng trên mặt đất rồi đo chiều dài bóng của cọc gỗ do ánh đèn điện tạo ra và đo khoảng cách từ điểm E đến chân cột đèn (điểm B). Theo em bác Dương đa tính như thế nào để ra được chiều cao cột đèn?
Bài 33. Hai tam giác đồng dạng
QL
Hướng dẫn giải
Thảo luận (1)
QL
Trong hình 9.2, ΔABC và ΔABC là hai tam giác có các cạnh tương ứng song song và các góc tương ứng bằng nhau, tức là AB // DE, AC // DF, BC // EF và widehat A widehat D{,^{}}widehat B widehat E{;^{}}widehat C widehat FNhìn hình vẽ, hãy cho biết giá trị các tỉ số sau: frac{{AB}}{{DE}}{;^{}}frac{{BC}}{{EF}}{;^{}}frac{{AC}}{{DF}}
Đọc tiếp
Trong hình 9.2, ΔABC và ΔABC là hai tam giác có các cạnh tương ứng song song và các góc tương ứng bằng nhau, tức là AB // DE, AC // DF, BC // EF và \(\widehat A = \widehat D{,^{}}\widehat B = \widehat E{;^{}}\widehat C = \widehat F\)
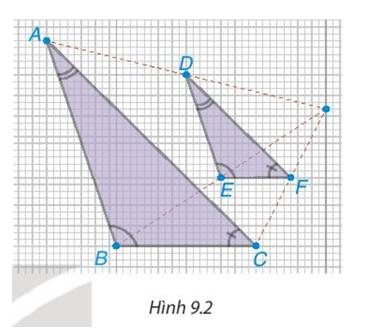
Nhìn hình vẽ, hãy cho biết giá trị các tỉ số sau: \(\frac{{AB}}{{DE}}{;^{}}\frac{{BC}}{{EF}}{;^{}}\frac{{AC}}{{DF}}\)
Hướng dẫn giải
Thảo luận (2)
Ta có: \(\frac{{AB}}{{DE}} = 2{;^{}}\frac{{BC}}{{EF}} = 2{;^{}}\frac{{AC}}{{DF}} = 2\)
Trả lời bởi Hà Quang Minh
QL
Trong các tam giác được vẽ trên ô lưới vuông, có một cặp tam giác đồng dạng. Hãy chỉ ra cặp tam giác đó, viết đúng kí hiệu đồng dạng và tìm tỉ số đồng dạng của chúng.
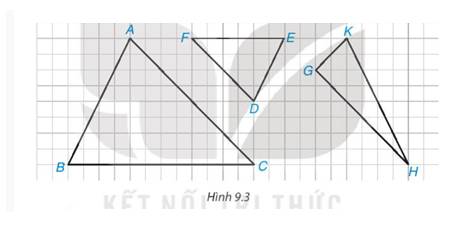
Hướng dẫn giải
Thảo luận (1)
ΔABC \(\backsim\) ΔDEF với tỉ số đồng dạng là \(\frac{1}{2}\)
Trả lời bởi Hà Quang Minh
QL
Cho \(\Delta ABC \backsim \Delta MNP\). Chứng minh rằng:
a) Nếu tam giác ABC cân tại A thì tam giác MNP cân tại đỉnh M.
b) Nếu tam giác ABC đều thì tam giác MNP đều.
c) Nếu \(AB \ge AC \ge BC\) thì \(MN \ge MP \ge NP\)
Hướng dẫn giải
Thảo luận (1)
a) Tam giác ABC tại A nên \(\widehat B = \widehat C\) (1)
Vì \(\Delta ABC \backsim \Delta MNP\) nên \(\widehat A = \widehat M{;^{}}\widehat B = \widehat N{;^{}}\widehat C = \widehat P\) (2)
Từ (1) và (2) nên \(\widehat N = \widehat P\) suy ra tam giác MNP cân tại M.
b) Vì tam giác ABC là tam giác đều nên \(\widehat A = \widehat B = \widehat C = {60^o}\)(3)
Vì \(\Delta ABC \backsim \Delta MNP\) nên \(\widehat A = \widehat M{;^{}}\widehat B = \widehat N{;^{}}\widehat C = \widehat P\) (4)
Từ (3) và (4) suy ra \(\widehat M = \widehat N = \widehat P = {60^o}\) nên tam giác MNP là tam giác đều.
c) Vì tam giác ABC có \(AB \ge AC \ge BC\) suy ra \(\widehat C \ge \widehat B \ge \widehat A\) (quan hệ giữa góc và cạnh đối điện) (5)
Mà \(\Delta ABC \backsim \Delta MNP\) nên \(\widehat A = \widehat M{;^{}}\widehat B = \widehat N{;^{}}\widehat C = \widehat P\) (6)
Từ (5) và (6) suy ra \(\widehat P \ge \widehat N \ge \widehat M\) nên \(MN \ge MP \ge NP\)
Trả lời bởi Hà Quang Minh
QL
Cho ΔABC \(\backsim\) ΔMNP, khẳng định nào sau đây không đúng?
a) ΔMNP \(\backsim\) ΔABC
b) ΔBCA \(\backsim\) ΔNPM
c) ΔCAB \(\backsim\) ΔPNM
d) ΔACB \(\backsim\) ΔMNP
Hướng dẫn giải
Thảo luận (1)
QL
Khẳng định nào sau đây là đúng?
a) Hai tam giác bằng nhau thì đồng dạng với nhau.
b) Hai tam giác bất kì đồng dạng với nhau
c) Hai tam giác đều bất kì đồng dạng với nhau
d) Hai tam giác vuông bất kì đồng dạng với nhau
e) Hai tam giác đồng dạng thì bằng nhau
Hướng dẫn giải
Thảo luận (1)
Khẳng định a và c là khẳng định đúng
Khẳng định b sai vì hai tam giác gọi là đồng dạng với nhau nếu chúng có ba cặp góc bằng nhau từng đôi một và ba cặp cạnh tương ứng tỉ lệ.
Khẳng định d sai vì hai tam giác vuông mới chỉ thỏa mãn một điều kiện để xét đồng dạng, cần thêm tỉ lệ cạnh tương ứng hoặc 1 góc tương ứng bằng nhau.
Khẳng định e sai vì hai tam giác đồng dạng chỉ có kích thước tỉ lệ với nhau, còn hai tam giác bằng nhau là có các góc, các cạnh tương ứng bằng nhau
Trả lời bởi Hà Quang Minh
QL
Trong hình 9.9, ABC là tam giác không cân; M, N, P lần lượt là trung điểm của BC, CA, AB. Hãy tìm trong hình năm tam giác khác nhau mà chúng đôi một đồng dạng với nhau. Giải thích vì sao chúng đồng dạng.
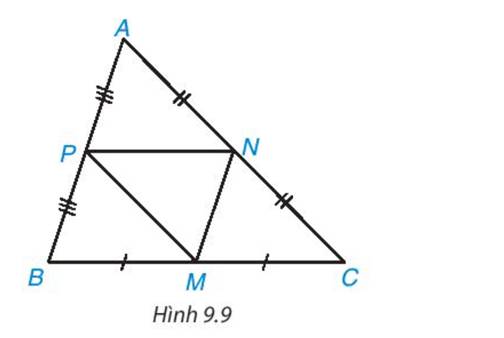
Hướng dẫn giải
Thảo luận (1)
- Có AP = BP, NA = NC
=> NP // BC (P ∈ AB, N ∈ AC)
=> ΔABC \(\backsim\) ΔAPN
- Có AP = BP, MB = MC
=> MP // AC (P ∈ AB, M ∈ BC)
=> ΔABC \(\backsim\) ΔPBM
- Có NA = NC, MB = MC
=> MN // AB (N ∈ AC,M ∈ BC)
=> ΔABC \(\backsim\) ΔNMC
- Có ΔABC \(\backsim\) ΔAPN và ΔABC \(\backsim\) ΔPBM => ΔAPN \(\backsim\) ΔPBM
- Có ΔABC \(\backsim\) ΔNMC và ΔABC \(\backsim\) ΔPBM => ΔNMC \(\backsim\) ΔPBM
Trả lời bởi Hà Quang Minh
QL
Cho tam giác ABC cân tại đỉnh A và tam giác MNP cân tại đỉnh M. Biết rằng \(\widehat {BAC} = \widehat {PMN}\), AB=2MN. Chứng minh ΔMNP ∽ ΔABC và tìm tỉ số đồng dạng
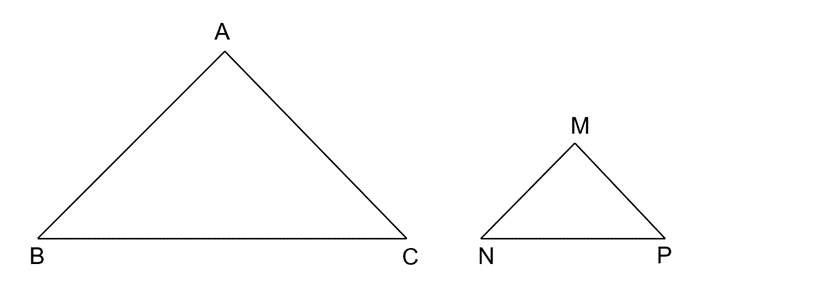
Hướng dẫn giải
Thảo luận (1)
- Có tam giác ABC cân tại A => AB = AC, \(\widehat B = \widehat C\)
- Có tam giác MNP cân tại M => MN = MP, \(\widehat N = \widehat P\)
Mà AB = 2MN, \(\widehat A = \widehat M\)
=> \(\widehat B = \widehat N = \widehat C = \widehat P\)
\( \Rightarrow \frac{{MN}}{{AB}} = \frac{{MP}}{{AC}} = \frac{{NP}}{{BC}} = \frac{1}{2}\)
=> ΔMNP ∽ ΔABC với tỉ số đồng dạng là \(\frac{1}{2}\)
Trả lời bởi Hà Quang Minh
Bác Dương đã chứng minh ΔAEB ∽ ΔDEC và tìm tỉ số đồng dạng của chúng từ đó tính được chiều cao của cột đèn
Trả lời bởi Hà Quang Minh