Dùng định nghĩa xét tính liên tục của hàm số \(f\left(x\right)=x^3+2x-1\) tại \(x_o=3\) ?
a) Xét tính liên tục của hàm số \(y=g\left(x\right)\) tại \(x_0=2\) biết :
\(g\left(x\right)=\left\{{}\begin{matrix}\dfrac{x^3-8}{x-2};\left(x\ne2\right)\\5;\left(x=2\right)\end{matrix}\right.\)
b) Trong biểu thức xác định \(g\left(x\right)\) ở trên, cần thay số 5 bởi số nào để hàm số liên tục tại \(x_0=2\)
a) Ta có 
= 22 +2.2 +4 = 12.
Vì 
nên hàm số y = g(x) gián đoạn tại x0 = 2.
b) Để hàm số y = f(x) liên tục tại x0 = 2 thì ta cần thay số 5 bởi số 12
Trả lời bởi Mai Hà ChiCho hàm số \(f\left(x\right)=\left\{{}\begin{matrix}3x+2;\left(x< -1\right)\\x^2-1;\left(x\ge-1\right)\end{matrix}\right.\)
a) Vẽ đồ thị hàm số \(y=f\left(x\right)\). Từ đó nêu nhận xét về tính liên tục của hàm số trên tập xác định của nó ?
b) Khẳng định nhận xét trên bằng một chứng minh ?
a) Các bạn tự vẽ hình nhé . Đồ thị hàm số y = f(x) là một đường không liền nét mà bị đứt quãng tại x0 = -1. Vậy hàm số đã cho liên tục trên khoảng (-∞; -1) và (- 1; +∞).
b) +) Nếu x < -1: f(x) = 3x + 2 liên tục trên (-∞; -1) (vì đây là hàm đa thức).
+) Nếu x> -1: f(x) = x2 – 1 liên tục trên (-1; +∞) (vì đây là hàm đa thức).
+) Tại x = -1;
Ta có =
= 3(-1) +2 = -1.
= (-1)2 – 1 = 0.
Vì 
nên không tồn tại 
. Vậy hàm số gián đoạn tại
x0 = -1.
Cho hàm số \(f\left(x\right)=\dfrac{x+1}{x^2+x-6}\) và \(g\left(x\right)=\tan x+\sin x\)
Với mỗi hàm số, hãy xác định các khoảng trên đó hàm số liên tục ?
+) Hàm số 
xác định khi và chỉ khi x2+ x – 6 ≠ 0 <=> x ≠ -3 và x ≠ 2.
Hàm số f(x) liên tục trên các khoảng (-∞; -3), (-3; 2) và (2; +∞)
+) Hàm số g(x) = tanx + sinx xác định khi và chỉ khi
tanx ≠ 0 <=> x ≠ π/2 +kπ với k ∈ Z.
Hàm số g(x) liên tục trên các khoảng ( – π/2+kπ; π/2 +kπ) với k ∈ Z.
Trả lời bởi Mai Hà ChiÝ kiến sau đúng hay sai ?
"Nếu hàm số \(y=f\left(x\right)\) liên tục tại điểm \(x_0\) còn hàm số \(y=g\left(x\right)\) không liên tục tại \(x_0\), thì \(y=f\left(x\right)+g\left(x\right)\) là một hàm số không liên tục tại \(x_0\)"
Ý kiến đúng
Giả sử ngược lại y = f(x) + g(x) liên tục tại x0. Đặt h(x) = f(x) + g(x). Ta có g(x) = h(x) – f(x).
Vì y = h(x) và y = f(x) liên tục tại x0 nên hiệu của chúng là hàm số y = g(x) phải liên tục tại x0. Điều này trái với giả thiết là y = g(x) không liên tục tại x0.
Trả lời bởi Mai Hà ChiChứng minh rằng phương trình :
a) \(2x^2-6x+1=0\) có ít nhất hai nghiệm
b) \(\cos x=x\) có nghiệm
a) Hàm số f(x) = 2x3 + 6x + 1 là hàm đa thức nên liên tục trên R.
Mặt khác vì f(0).f(1) = 1.(-3) < 0 nên phương trình có nghiệm trong khoảng (1; 2).
Vậy phương trình f(x) = 0 có ít nhất hai nghiệm.
b) Hàm số g(x) = cosx – x xác định trên R nên liên tục trên R.
Mặt khác, ta có g(0).g(π/2) = 1. (-π/2) < 0 nên phương trình đã cho có nghiệm trong khoảng (0; π/2).
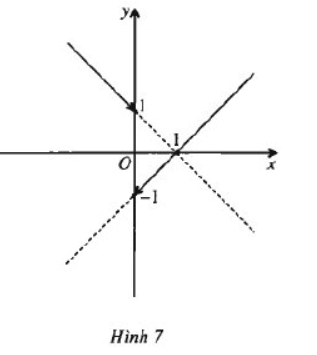
Trả lời bởi Mai Hà ChiCho hàm số \(f\left(x\right)=\dfrac{\left(x-1\right)\left|x\right|}{x}\)
Vẽ đồ thị của hàm số này. Từ đồ thị dự đoán các khoảng trên đó hàm số liên tục và chứng minh dự đoán đó ?
Cho ví dụ về một hàm số liên tục trên (a; b] và trên (b;c) nhưng không liên tục trên (a; c) ?
Chứng minh rằng nếu một hàm số liên tục trên (a;b] và trên [b; c) thì nó liên tục trên (a; c) ?
Cho hàm số \(y=f\left(x\right)\) xác định trên khoảng (a; b) chứa điểm \(x_0\)
Chứng minh rằng nếu \(\lim\limits_{x\rightarrow x_0}\dfrac{f\left(x\right)-f\left(x_0\right)}{x-x_0}=L\) thì hàm số \(f\left(x\right)\) liên tục tại điểm \(x_0\) ?
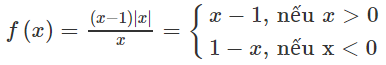
Hàm số f(x) = x3 + 2x - 1 xác định trên R và x0 = 3 ∈ R.
nên hàm số đã cho liên tục tại điểm x0 = 3.
Trả lời bởi Đặng Phương Nam