Tính \(\cos \frac{{7\pi }}{{12}} + \cos \frac{\pi }{{12}}\)
Bài 3. Các công thức lượng giác
H24
Hướng dẫn giải
Thảo luận (1)
H24
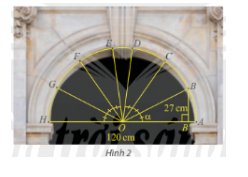
Trong bài toán khởi động, cho biết vòm cổng rộng 120 cm và khoảng cách từ B đến đường kính AH là 27 cm. Tính \(\sin \alpha \) và \(\cos \alpha \), từ đó tính khoảng cách từ điểm C đến đường kính AH. Làm tròn kết quả đến hàng phần mười.
Hướng dẫn giải
Thảo luận (1)
Ta có: \(OA = OB = 120:2 = 60\)
Xét tam giác OBB’ có:
\(\sin \widehat {BOB'} = \frac{{BB'}}{{OB}} = \frac{{27}}{{60}} = \frac{9}{{20}}\)
\(\widehat {AOC} = 2\widehat {BOB'}\)
(Vì số đo cung AC gấp 2 lần số đo cung AB)
Xét tam giác OCC’ vuông tại C’ có:
\(\begin{array}{l}\sin \widehat {COC'} = \frac{{CC'}}{{OC}}\\ \Leftrightarrow CC' = OC.\sin \widehat {COC'} = OC.\sin \left( {2\widehat {BOB'}} \right)\end{array}\)
Mà \(\sin \left( {2\widehat {BOB'}} \right) = 2.\sin \widehat {BOB'}.cos\widehat {BOB'}\)
\( = 2.\frac{9}{{20}}.\frac{{\sqrt {319} }}{{20}} = \frac{{9\sqrt {319} }}{{400}}\)
Vậy khoảng cách từ C đến AH là \(60.\frac{{9\sqrt {319} }}{{200}} \approx 48,2cm\).
Trả lời bởi Quoc Tran Anh Le
H24
Tính \(\cos \frac{\pi }{8}\) và \(\tan \frac{\pi }{8}\)
Hướng dẫn giải
Thảo luận (1)
Ta có:
\(\begin{array}{l}cos\left( {\frac{\pi }{4}} \right) = cos\left( {2.\frac{\pi }{8}} \right) = 2co{s^2}\frac{\pi }{8} - 1 = \frac{{\sqrt 2 }}{2}\\ \Rightarrow co{s^2}\frac{\pi }{8} = \frac{{\sqrt 2 + 2}}{4}\end{array}\)
\( \Rightarrow cos\frac{\pi }{8} = \sqrt {\frac{{\sqrt 2 + 2}}{4}} = \frac{{\sqrt {\sqrt 2 + 2} }}{2}\) (vì \(0 < \frac{\pi }{8} < \frac{\pi }{2}\))
Ta có:
\(\tan \left( {\frac{\pi }{4}} \right) = \tan \left( {2.\frac{\pi }{8}} \right) = \frac{{2\tan \frac{\pi }{8}}}{{1 - {{\tan }^2}\frac{\pi }{8}}} = 1\)
\(\begin{array}{l} \Leftrightarrow 1 - {\tan ^2}\frac{\pi }{8} = 2\tan \frac{\pi }{8}\\ \Leftrightarrow {\tan ^2}\frac{\pi }{8} + 2\tan \frac{\pi }{8} - 1 = 0\end{array}\)
\( \Leftrightarrow \tan \frac{\pi }{8} = - 1 + \sqrt 2 \)(vì \(0 < \frac{\pi }{8} < \frac{\pi }{2}\))
Trả lời bởi Quoc Tran Anh Le
H24
Áp dụng công thức biến đổi tích thành tổng cho hai góc lượng giác \(\alpha = \frac{{\alpha + \beta }}{2},\beta = \frac{{\alpha - \beta }}{2}\) ta được đẳng thức nào?
Hướng dẫn giải
Thảo luận (1)
Ta có:
\(\begin{array}{l}\cos \alpha \cos \beta = \cos \frac{{\alpha + \beta }}{2}\cos \frac{{\alpha - \beta }}{2}\\ = \frac{1}{2}\left[ {\cos \left( {\frac{{\alpha + \beta }}{2} + \frac{{\alpha - \beta }}{2}} \right) + \cos \left( {\frac{{\alpha + \beta }}{2} - \frac{{\alpha - \beta }}{2}} \right)} \right]\\ = \frac{1}{2}\left( {\cos \alpha + \cos \beta } \right)\end{array}\)
\(\begin{array}{l}\sin \alpha \sin \beta = \sin \frac{{\alpha + \beta }}{2}\sin \frac{{\alpha - \beta }}{2}\\ = \frac{1}{2}\left[ {\cos \left( {\frac{{\alpha + \beta }}{2} - \frac{{\alpha - \beta }}{2}} \right) - \cos \left( {\frac{{\alpha + \beta }}{2} + \frac{{\alpha - \beta }}{2}} \right)} \right]\\ = \frac{1}{2}\left( {\cos \beta - \cos \alpha } \right)\end{array}\)
\(\begin{array}{l}\sin \alpha \cos \beta = \sin \frac{{\alpha + \beta }}{2}\cos \frac{{\alpha - \beta }}{2}\\ = \frac{1}{2}\left[ {\sin \left( {\frac{{\alpha + \beta }}{2} + \frac{{\alpha - \beta }}{2}} \right) + \sin \left( {\frac{{\alpha + \beta }}{2} - \frac{{\alpha - \beta }}{2}} \right)} \right]\\ = \frac{1}{2}\left( {\sin \alpha + \sin \beta } \right)\end{array}\)
Trả lời bởi Quoc Tran Anh Le
H24
Từ công thức cộng, hãy tính tổng và hiệu của:
a) \(\cos \left( {\alpha - b} \right)\) và \(\cos \left( {\alpha + \beta } \right)\);
b) \(\sin \left( {\alpha - \beta } \right)\)và \(\sin \left( {\alpha + \beta } \right)\).
Hướng dẫn giải
Thảo luận (1)
a,
\(\begin{array}{l}\cos \left( {\alpha - b} \right) + \cos \left( {\alpha + \beta } \right)\\ = \cos \alpha \cos \beta + \sin \alpha sin\beta + \cos \alpha \cos \beta - \sin \alpha sin\beta \\ = 2\cos \alpha \cos \beta \end{array}\)
\(\begin{array}{l}\cos \left( {\alpha - b} \right) - \cos \left( {\alpha + \beta } \right)\\ = \cos \alpha \cos \beta + \sin \alpha sin\beta - \cos \alpha \cos \beta + \sin \alpha sin\beta \\ = 2\sin \alpha sin\beta \end{array}\)
b,
\(\begin{array}{l}\sin \left( {\alpha - \beta } \right) - \sin \left( {\alpha + \beta } \right)\\ = \sin \alpha \cos \beta - \cos \alpha sin\beta - \sin \alpha \cos \beta - \cos \alpha sin\beta \\ = - 2\cos \alpha sin\beta \end{array}\)
\(\begin{array}{l}\sin \left( {\alpha - \beta } \right) + \sin \left( {\alpha + \beta } \right)\\ = \sin \alpha \cos \beta - \cos \alpha sin\beta + \sin \alpha \cos \beta + \cos \alpha sin\beta \\ = 2\sin \alpha \cos \beta \end{array}\)
Trả lời bởi Quoc Tran Anh Le
H24
Hãy áp dụng công thức cộng cho trường hợp β = α và tính các giá trị lượng giác của góc 2α.
Hướng dẫn giải
Thảo luận (1)
\(\begin{array}{l}\cos \left( {\alpha + \alpha } \right) = \cos 2\alpha = \cos \alpha \cos \alpha - \sin \alpha sin\alpha = {\cos ^2}\alpha - {\sin ^2}\alpha \\ = {\cos ^2}\alpha + {\sin ^2}\alpha - 2{\sin ^2}\alpha = 1 - 2{\sin ^2}\alpha = 2{\cos ^2}a - 1\end{array}\)
\(\tan 2\alpha = \tan \left( {\alpha + \alpha } \right) = \frac{{\tan \alpha + \tan \alpha }}{{1 - \tan \alpha .\tan \alpha }} = \frac{{2\tan a}}{{1 - {{\tan }^2}a}}\)
Trả lời bởi Quoc Tran Anh Le
H24
Quan sát Hình 1. Từ hai cách tính tích vô hướng của vectơ overrightarrow {OM} ,overrightarrow {ON} sau đây:overrightarrow {OM} .overrightarrow {ON} left| {overrightarrow {OM} } right|.left| {overrightarrow {ON} } right|.cosleft( {overrightarrow {OM} ,overrightarrow {ON} } right) cosleft( {overrightarrow {OM} ,overrightarrow {ON} } right) cosleft( {alpha - beta } right)overrightarrow {OM} .overrightarrow {ON} {x_M}.{x_N} + {y_M}.{y_N}Hãy suy ra công thức tính cos(α – β) theo các giá trị l...
Đọc tiếp
Quan sát Hình 1. Từ hai cách tính tích vô hướng của vectơ \(\overrightarrow {OM} ,\overrightarrow {ON} \) sau đây:

\(\overrightarrow {OM} .\overrightarrow {ON} = \left| {\overrightarrow {OM} } \right|.\left| {\overrightarrow {ON} } \right|.cos\left( {\overrightarrow {OM} ,\overrightarrow {ON} } \right)\)\( = cos\left( {\overrightarrow {OM} ,\overrightarrow {ON} } \right) = cos\left( {\alpha - \beta } \right)\)
\(\overrightarrow {OM} .\overrightarrow {ON} = {x_M}.{x_N} + {y_M}.{y_N}\)
Hãy suy ra công thức tính cos(α – β) theo các giá trị lượng giác của α và β. Từ đó, hãy suy ra công thức cos(α + β) bằng cách thay β bằng – β.
Hướng dẫn giải
Thảo luận (1)
\(cos\left(\alpha-\beta\right)=x_M\cdot x_N=cos\alpha\cdot cos\beta+sin\alpha\cdot sin\beta\\ cos\left(\alpha+\beta\right)=cos\left[\alpha-\left(-\beta\right)\right]=cos\alpha\cdot cos\left(-\beta\right)+sin\alpha\cdot sin\left(-\beta\right)=cos\alpha\cdot cos\beta-sin\alpha\cdot sin\beta\)
Trả lời bởi Hà Quang Minh
H24
Trong kiến trúc, các vòm cổng bằng đá thường có hình nửa đường tròn để có thể chịu lực tốt. Trong hình bên, vòm cổng được ghép bởi sáu phiến đá hai bên tạo thành các cung AB, BC, CD, EF, FG, GH bằng nhau và một phiến đá chốt ở đỉnh. Nếu biết chiều rộng cổng và khoảng cách từ điểm B đến đường kính AH, làm thế nào để tính được khoảng cách từ điểm C đến AH?
Đọc tiếp
Trong kiến trúc, các vòm cổng bằng đá thường có hình nửa đường tròn để có thể chịu lực tốt. Trong hình bên, vòm cổng được ghép bởi sáu phiến đá hai bên tạo thành các cung AB, BC, CD, EF, FG, GH bằng nhau và một phiến đá chốt ở đỉnh. Nếu biết chiều rộng cổng và khoảng cách từ điểm B đến đường kính AH, làm thế nào để tính được khoảng cách từ điểm C đến AH?

Hướng dẫn giải
Thảo luận (1)
H24
Tính \(\sin \frac{\pi }{{12}}\) và \(\tan \frac{\pi }{{12}}\)
Hướng dẫn giải
Thảo luận (1)
\(sin\left(\dfrac{\pi}{12}\right)=sin\left(\dfrac{\pi}{3}-\dfrac{\pi}{4}\right)=sin\dfrac{\pi}{3}cos\dfrac{\pi}{4}-cos\dfrac{\pi}{3}sin\dfrac{\pi}{4}=\dfrac{\sqrt{3}}{2}\cdot\dfrac{\sqrt{2}}{2}-\dfrac{1}{2}\cdot\dfrac{\sqrt{2}}{2}=\dfrac{\sqrt{6}-\sqrt{2}}{4}\\ cos\left(\dfrac{\pi}{12}\right)=\dfrac{\sqrt{6}+\sqrt{2}}{4}\\ tan\left(\dfrac{\pi}{12}\right)=\dfrac{sin\dfrac{\pi}{12}}{cos\dfrac{\pi}{12}}=\dfrac{\dfrac{\sqrt{6}-\sqrt{2}}{4}}{\dfrac{\sqrt{6}+\sqrt{2}}{4}}=2-\sqrt{3}\)
Trả lời bởi Hà Quang Minh
H24
Tính giá trị của các biểu thức\(\sin \frac{\pi }{{24}}\cos \frac{{5\pi }}{{24}}\) và \(\sin \frac{{7\pi }}{8}\sin \frac{{5\pi }}{8}\)
Hướng dẫn giải
Thảo luận (1)
Ta có:
\(\begin{array}{l}\sin \frac{\pi }{{24}}\cos \frac{{5\pi }}{{24}} = \frac{1}{2}\left[ {\sin \left( {\frac{\pi }{{24}} + \frac{{5\pi }}{{24}}} \right) + \sin \left( {\frac{\pi }{{24}} - \frac{{5\pi }}{{24}}} \right)} \right]\\ = \frac{1}{2}\left[ {\sin \left( {\frac{\pi }{4}} \right) + \sin \left( { - \frac{\pi }{6}} \right)} \right]\\ = \frac{1}{2}\left[ {\frac{{\sqrt 2 }}{2} - \frac{1}{2}} \right] = \frac{{\sqrt 2 - 1}}{4}\end{array}\)
Ta có:
\(\begin{array}{l}\sin \frac{{7\pi }}{8}\sin \frac{{5\pi }}{8} = \frac{1}{2}\left[ {\cos \left( {\frac{{7\pi }}{8} - \frac{{5\pi }}{8}} \right) - \cos \left( {\frac{{7\pi }}{8} + \frac{{5\pi }}{8}} \right)} \right]\\ = \frac{1}{2}\left[ {\cos \left( {\frac{\pi }{4}} \right) - \cos \left( {\frac{{3\pi }}{2}} \right)} \right]\\ = \frac{1}{2}.\left( {\frac{{\sqrt 2 }}{2} + 0} \right) = \frac{{\sqrt 2 }}{4}\end{array}\)
Trả lời bởi Quoc Tran Anh Le
\(cos\dfrac{7\pi}{12}+cos\dfrac{\pi}{12}\\ =2.cos\dfrac{\dfrac{7\pi}{12}+\dfrac{\pi}{12}}{2}\\ =2.cos\dfrac{\pi}{3}.cos\dfrac{\pi}{4}\\ =2.\dfrac{1}{2}.\dfrac{\sqrt{2}}{2}\\ =\dfrac{\sqrt{2}}{2}\)
Trả lời bởi Mai Trung Hải Phong