Khái niệm tập hợp thường gặp trong toán học và đời sống. Chẳng hạn:
- Tập hợp A các học sinh của lớp 10D.
- Tập hợp B các học sinh tổ I của lớp đó.
Làm thế nào để diễn tả mối quan hệ giữa tập hợp A và tập hợp B?
Khái niệm tập hợp thường gặp trong toán học và đời sống. Chẳng hạn:
- Tập hợp A các học sinh của lớp 10D.
- Tập hợp B các học sinh tổ I của lớp đó.
Làm thế nào để diễn tả mối quan hệ giữa tập hợp A và tập hợp B?
Ở lớp 6, ta đã làm quen với khái niệm tập hợp, kí hiệu và cách viết tập hợp, phần tử thuộc tập hợp. Hãy nêu cách cho một tập hợp.
Có hai cách cho một tập hợp:
+) Liệt kê các phần tử của tập hợp.
Chẳng hạn: A = {0; 1; 2; 3; 4; 5}
+) Chỉ ra tính chất đặc trưng của tập hợp đó.
Chẳng hạn: A = {\(x \in \mathbb{N}|0 \le x \le 5\)}
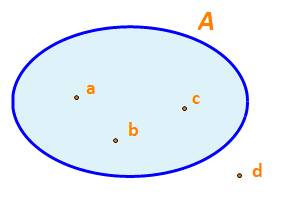
Trả lời bởi Hà Quang MinhNgười ta còn minh họa tập hợp bằng một vòng kín, mỗi phần tử của tập hợp được biểu diễn bởi một chấm bên trong vòng kín, còn phần tử không thuộc tập hợp đó được biểu diễn bởi một chấm bên ngoài vòng kín (Hình 1). Cách minh họa tập hợp như vậy được gọi là biểu đồ Ven.
a) Viết tập hợp A trong Hình 1 bằng cách liệt kê các phần tử của các tập hợp đó.
b) Nêu phần tử không thuộc tập hợp A
Nêu số phần tử của mỗi tập hợp sau:
\(C = \{ x \in \mathbb{R}|{x^2} < 0\} ,\) \(D = \{ a\} ,E = \{ b;c;d\} ,\)\(\mathbb{N} = \left\{ {0;1;2;..} \right\}\)
\(C = \{ x \in \mathbb{R}|{x^2} < 0\} \). Tập hợp C không chứa phần tử nào vì bình phương mọi số thực đều không âm.
\(D = \{ a\} ,\) tập hợp D có duy nhất 1 phần tử là a.
\(E = \{ b;c;d\} ,\) tập hợp E có 3 phần tử.
\(\mathbb{N} = \left\{ {0;1;2;..} \right\}\): tập hợp N có vô số phần tử.
Trả lời bởi Hà Quang MinhNêu số phần tử của mỗi tập hợp sau:
\(G = \{ x \in \mathbb{Z}|{x^2} -2 = 0\} ,\) \(\mathbb{N}* = \left\{ {1;2;3;..} \right\}.\)
\(G = \{ x \in \mathbb{Z}|{x^2} -2 = 0\} \). Tập hợp G không chứa phần tử nào vì \({x^2} - 2 = 0 \Leftrightarrow x = \pm \sqrt 2 \notin \mathbb{Z}\)
\(\mathbb{N}* = \left\{ {1;2;3;..} \right\}.\): tập hợp N* có vô số phần tử.
Trả lời bởi Hà Quang MinhCho hai tập hợp:
\(A = \{ x \in \mathbb{Z}| - 3 < x < 3\} ,\)\(B = \{ x \in \mathbb{Z}| - 3 \le x \le 3\} \)
a) Viết tập hợp A, B bằng cách liệt kê các phần tử của tập hợp.
b) Mỗi phần tử của tập hợp A có thuộc tập hợp B không?
a) \(A = \{ - 2; - 1;0;1;2\} \)
\(B = \{ - 3; - 2; - 1;0;1;2;3\} \)
b) Mỗi phần tử của tập hợp A đều thuộc tập hợp B.
Trả lời bởi Hà Quang MinhCho hai tập hợp:
\(A = \{ n \in N|n\)chia hết cho 3},
\(B = \{ n \in N|n\)chia hết cho 9}.
Chứng tỏ rằng \(B \subset A.\)
Lấy n bất kì thuộc tập hợp B.
Ta có: n chia hết cho 9 \( \Rightarrow n = 9k\;\;(k \in \mathbb{N})\)
\( \Rightarrow n = 3.(3k)\;\; \vdots \;3\;\;(k \in \mathbb{N})\)
\( \Rightarrow n \in A\)
Như vậy, mọi phần tử của tập hợp B đều là phần tử của tập hợp A hay \(B \subset A.\)
Trả lời bởi Hà Quang MinhCho hai tập hợp:
\(A = \{ 0;6;12;18\},\)
\(B = \{ n \in N|\, n \le 18\) và n là bội của 6}.
Các mệnh đề sau có đúng không?
a) \(A \subset B.\)
b) \(B \subset A.\)
a) Nếu n là bội chung của 2 và 3 thì n là bội của 6, hay \(n \in B\)
Vậy mệnh đề \(A \subset B\) đúng.
b) Nếu n là bội 6 thì n vừa là bội của 2 vừa là bội của 3.
Do đó n là bội chung của 2 và 3 hay \(n \in A\).
Vậy mệnh đề \(A \subset B\) đúng.
Trả lời bởi Hà Quang MinhCho hai tập hợp:
\(E = \{ n \in N|n\) chia hết cho 3 và 4}, và \(G = \{ n \in N|n\) chia hết cho 12}.
Chứng tỏ rằng E = G.
Ta có:
n chia hết cho 3 và 4 \( \Leftrightarrow \)n chia hết cho 12 (do (3,4) =1)
Do đó: nếu n là phần tử của tập hợp A thì n cũng là phần tử của tập hợp B và ngược lại.
Hay mọi phần tử của tập hợp A đều là phần tử của tập hợp B và ngược lại.
Vậy \(E \subset G\) và \(G \subset E\) hay E = G.
Trả lời bởi Hà Quang MinhLớp trưởng lập hai danh sách các bạn đăng kí tham gia câu lạc bộ thể thao như sau (biết trong lớp không có hai bạn nào cùng tên):
- Bóng đá gồm: An, Bình, Chung, Dũng, Minh, Nam, Phương.
- Bóng rổ gồm: An, Chung, Khang, Phong, Quang, Tuấn.
Hãy liệt kê danh sách các bạn đăng kí tham gia cả hai câu lạc bộ.
Danh sách các bạn đăng kí tham gia cả hai câu lạc bộ là: An, Chung.
Trả lời bởi Hà Quang Minh
Vì các học sinh tổ I đều là các học sinh lớp 10D nên tập hợp B là tập con của tập hợp A.
Kí hiệu: \(B \subset A\)
Trả lời bởi Hà Quang Minh