Đáp án A
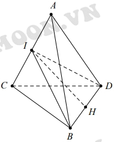 Gọi I, H lần lượt là trung điểm AC, BD. Ta có
B
I
⊥
A
C
D
I
⊥
A
C
⇒
A
C
⊥
I
B
D
và
V
I
.
B
C
D
=
V
I
.
A
B
D
Gọi I, H lần lượt là trung điểm AC, BD. Ta có
B
I
⊥
A
C
D
I
⊥
A
C
⇒
A
C
⊥
I
B
D
và
V
I
.
B
C
D
=
V
I
.
A
B
D
Lại có I B = A B 2 - A I 2 = 1 - x 2 4 ,với AC = BD = x.
Và I H = I B 2 - B H 2 = 1 - x 2 4 - x 2 4 = 1 - x 2 2
Diện tích tam giác IBD là S ∆ I B D = 1 2 I H . B D = x 2 1 - x 2 2
Suy ra V A B C D = 2 V I . B C D = 2 3 I C . S I B D = x 3 . x 2 1 - x 2 2 = x 2 6 1 - x 2 2
Xét hàm số f x = x 2 2 - x 2 → m a x f x = 4 6 9
Vậy thể tích lớn nhất là V m a x = 4 6 9 : 6 2 = 2 3 27

