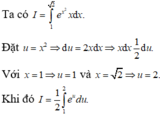Các câu hỏi tương tự
Câu 1:(0,5đ)Liệt kê các phần tử của tập hợp A {x ∈ N/15 ≤ x ≤ 19}Câu 2: (3đ) thực hiện phép tínha. 2.(72 – 2.32) – 60b. 27.63 + 27.37c. l-7l + (-8) + l-11l + 2d. 568 – 34 {5.l9 – ( 4-1)2l + 10}Câu 3: ( 2,5 điểm ) Tìm số nguyên xa) 2x + 3 52 : 5b) 105 – ( x + 7) 27 : 25Câu 4 (1 điểm): Học sinh lớp 6B khi xếp hàng 2, hàng 4, hàng 8 đều vừa đủ hàng. Biết số học sinh lớp đó trong khoảng 30 đến 38. Tính số học sinh của lớp 6B.Câu 5:(1 điểm) Khi nào thì M là trung điểm của đoạn thẳng AB? Vẽ...
Đọc tiếp
Câu 1:(0,5đ)
Liệt kê các phần tử của tập hợp A = {x ∈ N/15 ≤ x ≤ 19}
Câu 2: (3đ) thực hiện phép tính
a. 2.(72 – 2.32) – 60
b. 27.63 + 27.37
c. l-7l + (-8) + l-11l + 2
d. 568 – 34 {5.l9 – ( 4-1)2l + 10}
Câu 3: ( 2,5 điểm ) Tìm số nguyên x
a) 2x + 3 = 52 : 5
b) 105 – ( x + 7) = 27 : 25
Câu 4 (1 điểm): Học sinh lớp 6B khi xếp hàng 2, hàng 4, hàng 8 đều vừa đủ hàng. Biết số học sinh lớp đó trong khoảng 30 đến 38. Tính số học sinh của lớp 6B.
Câu 5:(1 điểm) Khi nào thì M là trung điểm của đoạn thẳng AB? Vẽ hình minh họa.
Câu 6: ( 2 điểm )Vẽ tia Ox, trên Ox lấy điểm A và B sao cho OA= 4cm, OB = 8cm.
a. Trong 3 điểm O, A, B điểm nào nằm giữa 2 điểm còn lại. Vì sao? . So sánh OA và AB
b. A có phải là trung điểm của OB không? Vì sao ?
Với cách biến đổi
u
1
+
3
ln
x
thì tích phân
∫
1
e
ln
x
x
1
+
3
ln
x
d
x
trở thành A.
2...
Đọc tiếp
Với cách biến đổi u = 1 + 3 ln x thì tích phân ∫ 1 e ln x x 1 + 3 ln x d x trở thành
A. 2 3 ∫ 1 2 u 2 − 1 d u
B. 2 9 ∫ 1 2 u 2 − 1 d u
C. 2 ∫ 1 2 u 2 − 1 d u
D. 9 2 ∫ 1 2 u 2 − 1 u d u
Cho nguyên hàm
I
∫
x
1
+
2
x
2
d
x
, khi thực hiện đổi biến số
u
1
+
2
x
2
thì ta được nguyên hàm theo biến số mới u là? A.
I
1
2
∫...
Đọc tiếp
Cho nguyên hàm I = ∫ x 1 + 2 x 2 d x , khi thực hiện đổi biến số u = 1 + 2 x 2 thì ta được nguyên hàm theo biến số mới u là?
A. I = 1 2 ∫ u 2 d u
B. I = ∫ u 2 d u
C. I = 2 ∫ u d u
D. I = ∫ u d u
Tích phân
I
∫
2
3
1
x
2
-
1
bằng với tích phân nào sau đây? A.
1
2
...
Đọc tiếp
Tích phân I = ∫ 2 3 1 x 2 - 1 bằng với tích phân nào sau đây?
A. 1 2 ∫ 2 3 ( 1 x + 1 - 1 x - 1 ) d x
B. 1 2 ∫ 2 3 ( - 1 x + 1 + 1 x - 1 ) d x
C. ∫ 2 3 ( 1 x + 1 - 1 x - 1 ) d x
D. ∫ 2 3 ( 1 x + 1 + 1 x - 1 ) d x
Một học sinh làm bài tích phân
I
∫
0
1
d
x
1
+
x
2
theo các bước sauBước 1: Đặt
x
tan
t
,
suy ra
d
x
1
+
tan...
Đọc tiếp
Một học sinh làm bài tích phân I = ∫ 0 1 d x 1 + x 2 theo các bước sau
Bước 1: Đặt x = tan t , suy ra d x = 1 + tan 2 t d t
Bước 2: Đổi x = 1 ⇒ t = π 4 , x = 0 ⇒ t = 0
Bước 3: I = ∫ 0 π 4 1 + tan 2 t 1 + tan 2 t d t = ∫ 0 π 4 d t = t 0 π 4 = 0 − π 4 = − π 4
Các bước làm trên, bước nào bị sai
A. Bước 3
B. Bước 2
C. Không bước nào sai cả
D. Bước 1
Tính
I
∫
x
s
inx
d
x
,
đặt
u
x
,
d
v
s
inx dx
.
Khi đó I biến đổi thành A.
I
−
x
c
osx-
∫
c
osx
d
x
B.
I
−
x
c
osx
+...
Đọc tiếp
Tính I = ∫ x s inx d x , đặt u = x , d v = s inx dx . Khi đó I biến đổi thành
A. I = − x c osx- ∫ c osx d x
B. I = − x c osx + ∫ c osx d x ,
C. I = x c osx + ∫ c osx d x ,
D. I = − x sin x + ∫ c osx d x
Câu 1: (2,5 điểm) Cho biểu thức:a) Rút gọn A.b) Tính giá trị của biểu thức A tại x thỏa mãn: 2x2 + x 0c) Tìm x để A 1/2d) Tìm x nguyên để A nguyên dương.Câu 2: (1điểm)a) Biểu diễn tập nghiệm của mỗi bất phương trình sau trên trục số: x ≥ -1 ; x 3.b) Cho a b, so sánh – 3a +1 với – 3b + 1.HD: a b -3a -3bCâu 3: (1,5 điểm) Một người đi xe đạp từ A đến B với vận tốc trung bình 15km/h. Lúc về, người đó chỉ đi với vận tốc trung bình 12km/h, nên thời gian về nhiều hơn thời gian đi l...
Đọc tiếp
Câu 1: (2,5 điểm) Cho biểu thức:
![]()
a) Rút gọn A.
b) Tính giá trị của biểu thức A tại x thỏa mãn: 2x2 + x = 0
c) Tìm x để A = 1/2
d) Tìm x nguyên để A nguyên dương.
Câu 2: (1điểm)
a) Biểu diễn tập nghiệm của mỗi bất phương trình sau trên trục số: x ≥ -1 ; x < 3.
b) Cho a < b, so sánh – 3a +1 với – 3b + 1.
HD: a < b => -3a > -3b
Câu 3: (1,5 điểm) Một người đi xe đạp từ A đến B với vận tốc trung bình 15km/h. Lúc về, người đó chỉ đi với vận tốc trung bình 12km/h, nên thời gian về nhiều hơn thời gian đi là 45 phút. Tính độ dài quãng đường AB (bằng kilômet).
HD: Đổi 45’ = ¾ h, quãng đường AB = S => S = vt hay S/15 = S/12+3/4
![]()
Câu 4: (1,0 điểm) Cho tam giác ABC có AD là phân giác trong của góc A. Tìm x trong hình vẽ sau với độ dài cho sẵn trong hình.
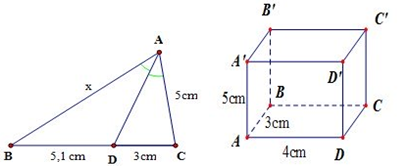
Câu 5: (1,5 điểm)
a. Viết công thức tính thể tích của hình hộp chữ nhật.
b. Áp dụng: Tính thể tích của hình hộp chữ nhật với AA’ = 5cm, AB = 3cm, AD = 4cm (hình vẽ trên).
Câu 6:(2,5 điểm) Cho tam giác ABC vuông tại A có AB = 6cm; AC = 8cm. Kẻ đường cao AH.
a) Chứng minh: ∆ABC và ∆HBA đồng dạng với nhau.
b) Chứng minh: AH2 = HB.HC.
c) Tính độ dài các cạnh BC, AH.
Bằng cách đặt
u
ln
x
,
d
v
x
2
d
x
thì tích phân
∫
1
2
x
2
ln
x
d
x
biến đổi thành kết quả nào sau đây? A.
x
3
ln...
Đọc tiếp
Bằng cách đặt u = ln x , d v = x 2 d x thì tích phân ∫ 1 2 x 2 ln x d x biến đổi thành kết quả nào sau đây?
A. x 3 ln x 3 1 3 − 1 3 ∫ 1 3 x 2 d x
B. x 2 ln x 2 1 3 − 1 3 ∫ 1 3 x 2 d x
C. x 3 ln x 3 1 3 + 1 3 ∫ 1 3 x 2 d x
D. − x 3 ln x 3 1 3 − 1 3 ∫ 1 3 x 2 d x
1. Từ A ngoài đường tròn tâm O. Kẻ 2 tia tiếp tuyến AM , AN. Biết góc MAN a độ ( không đổi ). Từ I bất kì trên cung nhỏ MN, vẽ tiếp tuyến cắt AM , AN tại B và C. OB và OC cắt đường tròn O tại D và E. CM : Cung DE không đổi khi I chạy trên cung MN2. Cho đường tròn O và O cắt nhau tại A và B. Qua A kẻ đường thẳng vuông góc với AB cắt đường tròn O tại C, cắt đường tròn O tại D. Tia CB cắt đường tròn O tại F , tia DB cắt đường tròn O tại E. CM : AB là tia phân giác góc EAF3. Cho tam giác ABC nhọn....
Đọc tiếp
1. Từ A ngoài đường tròn tâm O. Kẻ 2 tia tiếp tuyến AM , AN. Biết góc MAN = a độ ( không đổi ). Từ I bất kì trên cung nhỏ MN, vẽ tiếp tuyến cắt AM , AN tại B và C. OB và OC cắt đường tròn O tại D và E. CM : Cung DE không đổi khi I chạy trên cung MN
2. Cho đường tròn O và O' cắt nhau tại A và B. Qua A kẻ đường thẳng vuông góc với AB cắt đường tròn O tại C, cắt đường tròn O' tại D. Tia CB cắt đường tròn O' tại F , tia DB cắt đường tròn O tại E. CM : AB là tia phân giác góc EAF
3. Cho tam giác ABC nhọn. Điểm I bất kì trong tam giác. Kẻ IH vuông góc AB , IK vuông góc AC , IL vuông góc AB. Tìm vị trí điểm I sao cho : AL^2 + BH^2 + CK^2 đạt gtnn