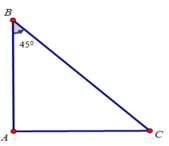
Tam giác ABC vuông tại A có ∠B = 45o ⇒ΔABC vuông cân tại A
⇒AB = AC ⇒AB/AC = 1
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
Xét tam giác ABC vuông tại A có ∠B α. Chứng minh rằng
a
)
α
45
°
⇔
AC
AB
1
b
)
α
60
°
⇔...
Đọc tiếp
Xét tam giác ABC vuông tại A có ∠B = α. Chứng minh rằng
a ) α = 45 ° ⇔ AC AB = 1 b ) α = 60 ° ⇔ AC AB = 3
Xét tam giác ABC vuông tại A có ∠B = α. Chứng minh rằng α = 60 o ⇔ A C A B = 3
Cho tam giác ABC vuông tại A, AB AC, cosC α
45
0
, đường trung tuyến AM, đường cao AH, MA MB MC α. Chứng minh:a, sin2α 2sin α.cos αb, 1 + cos2α 2
cos
2
α
c, 1 – cos2α 2
sin
2
α
Đọc tiếp
Cho tam giác ABC vuông tại A, AB < AC, cosC = α < 45 0 , đường trung tuyến AM, đường cao AH, MA = MB = MC = α. Chứng minh:
a, sin2α = 2sin α.cos α
b, 1 + cos2α = 2 cos 2 α
c, 1 – cos2α = 2 sin 2 α
1/ Cho tam giác ABC vuông tại B xét góc nhọn A =α hệ thức nào sai?
A. Sinα= BC/AC B. Cosα= AB/AC C. Tanα= BC/AC D. Cotα= AB/AC
Cho tam giác ABC có độ dài ba cạnh AB c, AC b, BA a và p là nửa chu vi của tam giác. Đường tròn tâm I nội tiếp tam giác lần lượt tiếp xúc với BC, AC và AB tại D, E và Fa, Chứng minh (I) có bán kính r (p – a)tan
B
A
C
^
2
b, Với
B
A
C
^...
Đọc tiếp
Cho tam giác ABC có độ dài ba cạnh AB = c, AC = b, BA = a và p là nửa chu vi của tam giác. Đường tròn tâm I nội tiếp tam giác lần lượt tiếp xúc với BC, AC và AB tại D, E và F
a, Chứng minh (I) có bán kính r = (p – a)tan B A C ^ 2
b, Với B A C ^ = α, tìm số đo của góc EDF theo α
c, Gọi H, K lần lượt là hình chiếu của B,C trên EF. Chứng minh: ∆BHF:∆CKE
d, Kẻ DP vuông góc vói EF tại P. Chứng minh: ∆FPB:∆CEP và PD là tia phân giác của góc B P C ^
Cho tam giác ABC vuông tại A, AB<AC, Ĉ = α < 45°, đường
trung tuyến AM, đường cao AH, MA=MB=MC=a. Chứng minh:
1+ cos2a = 2cos
2a
Cho △ ABC vuông tại A, có AB < AC và trung tuyến AM, góc ACB = α, góc AMB = β. Chứng minh rằng (sin α + cos a)2 = 1 + sin β
Cho tam giác ABC, đường phân giác AD. Biết AB=c, AC=b, ˆA=2α;(α<45o)A^=2α;(α<45o). Chứng minh AD=2bc.cosα/ b+c
Cho tam giác ABC vuông tại A; BC a không đổi,
C
^
α
0
0
α
90
0
Lập công thức để tính diện tích tam giác ABC theo a và A.
1
2
a
2
sin
...
Đọc tiếp
Cho tam giác ABC vuông tại A; BC = a không đổi, C ^ = α 0 0 < α < 90 0
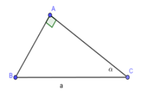
Lập công thức để tính diện tích tam giác ABC theo a và
A. 1 2 a 2 sin α . cos α
B. a 2 sin α . cos α
C. 2 a 2 sin α . cos α
D. 3 a 2 sin α . cos α