Đáp án D
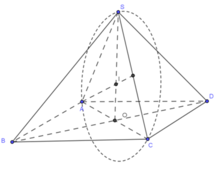
Gọi d = x ⇒ I O 2 = x − 9 2 .
Có O C = I C 2 − I O 2
= 9 2 − x − 9 2 = 18 x − x 2
⇒ A C = B D = 2 18 x − x 2
Vậy P = S O . S A B C D = x . 1 2 A C . B D
= 2 x . 18 x − x 2 = 2 x 2 18 − x
Có 36 = x + x + 2 18 − x
≥ 3 2 x 2 . 18 − x 3
⇒ x 2 18 − x ≤ 864.
Vậy P đạt giá trị lớn nhất khi x = 2 18 − x ⇔ x = 12 .

