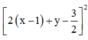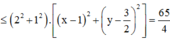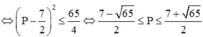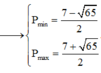Đáp án C.
Phương pháp giải: Dựa vào giả thiết, đánh giá đưa về tổng các bình phương, từ biểu thức P đưa về hạng tử trong tổng bình phương và áp dụng bất đẳng thức Bunhiacopxki tìm giá trị lớn nhất.
Lời giải:
Vì x2 + y2 > 1 suy ra log x 2 + y 2 f ( x ) là hàm số đồng biến trên tập xác định
Khi đó ![]()
![]()
![]()
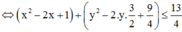
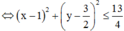
Xét biểu thức P, ta có 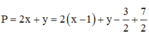
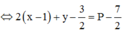
Áp dụng BĐT Bunhiacopxki, có