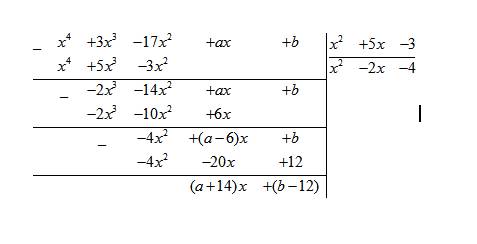
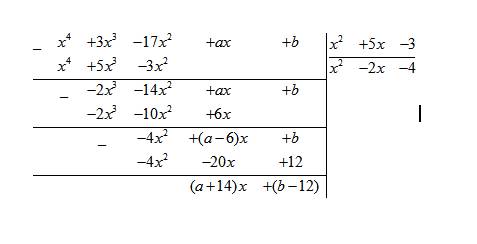
- Để \(f\left(x\right)\) chia hết cho \(g\left(x\right)\) thì:
\(\left\{{}\begin{matrix}a+14=0\\b-12=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-14\\b=12\end{matrix}\right.\)
Bài 1 :
Tìm tất cả cac số nguyên n để \(2n^2+n-7\) chia hết cho \(n-2\)
Bài 2 : Tìm các hằng số a và b sao cho đa thức f(x) chia hết cho đa thức g(x)
a) \(f\left(x\right)=\left(x^4+ax^2+b\right)\) ; \(g\left(x\right)=\left(x^2-x+1\right)\)
b) \(f\left(x\right)=ax^3+bx^2+5x-50\) ; \(g\left(x\right)=x^2+3x+3\)
Cho \(f\left(x\right)=6x^4-7x^3+ax^2+3x+2\) và \(g\left(x\right)=x^2-x+b\).Xác định a,b để f(x) chia hết cho g(x)
\(M=\left(1+\frac{a}{a^2+1}\right):\left(\frac{1}{a-1}-\frac{2a}{a^3-a^2+a-1}\right)\)
a)tìm điều kiện xác định
b)rút gọn M
Bài 2:
Cho f(x)=\(2x^2+\text{ax}+1v\text{à}g\left(x\right)=x-3\)
tìm a để f(x):g(x) dư 4
xác định các hệ số hữu tỉ a và b sao cho \(f\left(x\right)=x^4+ax^2+b\) chia hết cho \(g\left(x\right)=x^2-x-1\)
Câu 1: Cho f(x) = 6x4 – 7x3 + ax2 + 3x +2 và g(x) = x2 – x + b. Xác định a và b để f(x) chia hết cho g(x).
Câu 2:Chứng minh rằng với mọi số nguyên n , ta có \(A=\left[n^3\left(n^2-7\right)^2-36n\right]\) chia hết cho 7
1 . Tìm hệ số a để f(x) chia hết cho g(x) .
a , \(f\left(x\right)=x^3+3x^2+5x+a\)và \(g\left(x\right)=x+3\)
b, \(f\left(x\right)=x^3-3x+a\)và \(g\left(x\right)=x^2-2x+1\)
c , \(F\left(x\right)=x^4+5x^3-2x^2+ax+4\)và \(g\left(x\right)=x^2-3x+2\)
làm giúp mik bây giờ nhé mai mik đi học rồi làm xong mik tick cho nhé cảm ơn .
Xác định hệ số a, b để f(x) chia hết cho g(x), với:
\(f\left(x\right)=x^4+4\)
\(g\left(x\right)=x^2+ax+b\)
Tìm a, b sao cho \(f\left(x\right)=ax^3+bx^2+10x-4\) chia hết cho đa thức \(g\left(x\right)=x^2+x-2\)
xác định hằng số a và b sao cho
a)\(x^4+ax+b\)chia hết cho\(\left(x^2-4\right)\)
b)\(\left(x^3+ax+b\right)chiahetcho\left(x^2+2x-2\right)\)
c)\(x^4+ax^2+b\)chia hết cho\(\left(x^2-x+1\right)\)
d)\(x^4+ax^3+bx-1\)chia hết cho\(\left(x^2-1\right)\)
e) \(\left(ax^4+bx^3+1\right)\)chia hết cho\(\left(x-1\right)\)
f)\(ax^3+bx^2+5x-50\)chia hết cho\(\left(x^2+3x-10\right)\)
Xác định a, b để \(f\left(x\right)⋮g\left(x\right)\)
a) \(f\left(x\right)=2x^3-3x^2+ax+b\)
\(g\left(x\right)=x^2+x+2\)
b) \(f\left(x\right)=2x^4+ax^2+b\)
\(g\left(x\right)=x^2-x-3\)
c) \(f\left(x\right)=3x^4-8x^3-10x^2+ax-b\)
\(g\left(x\right)=3x^2-2x+1\)
d) \(f\left(x\right)=ax^3+bx^2-11x+30\)
\(g\left(x\right)=x^2-3x-10\)
