Đáp án B
Bổ đề. Cho hai số phức z1 và z2, ta luôn có
![]()
Chứng minh. Sử dụng công thức
![]()
Khi đó
![]()
![]()
![]()
Áp dụng (*), ta được
![]()
![]()
Theo bất đằng thức Bunhiacopxki, ta được
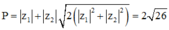
Đáp án B
Bổ đề. Cho hai số phức z1 và z2, ta luôn có
![]()
Chứng minh. Sử dụng công thức
![]()
Khi đó
![]()
![]()
![]()
Áp dụng (*), ta được
![]()
![]()
Theo bất đằng thức Bunhiacopxki, ta được
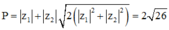
Với hai số phức z 1 và z 2 thỏa mãn z 1 + z 2 = 8 + 6 i và z 1 - z 2 = 2 . Tim giá trị lớn nhất của biểu thức P = | z 1 | + | z 2 | .
A. P=4 6
B. P=2 26
C. P=5+3 5
D. P=34+3 2
Cho hai số phức z 1 , z 2 thỏa mãn z 1 + 2 = 2 và z 2 - 3 i = z 2 + 1 - 6 i . Tìm giá trị nhỏ nhất của z 1 + z 2 .
A. - 10 + 6 10 5
B. 10 + 6 10 5
C. 0
D. 12 10
Cho hai số phức z 1 , z 2 thỏa mãn z 1 + z 2 = 3 5 + 4 5 i , | z 1 - z 2 | = 3 và biểu thức P = 4 | z 1 | 3 + 4 | z 2 | 3 - 3 | z 1 | - 3 | z 2 | + 5 đạt giá trị nhỏ nhất. Tính | z 1 | + | z 2 | .
A. 3
B. 3 4
C. 2
D. 1
Cho hai số thực z 1 , z 2 thỏa mãn z 1 + 5 = 5 và z 2 + 1 - 3 i = z 2 - 3 - 6 i . Tìm giá trị nhỏ nhất của z 1 - z 2
A. 5 2
B. 5 4
C. 10
D. 3
Cho 3 số phức z , z 1 , z 2 thỏa mãn z − 1 + 2 i = z + 3 − 4 i , z 1 + 5 − 2 i = 2 , z 2 − 1 − 6 i = 2. Tính giá trị nhỏ nhất của biểu thức T = z − z 1 + z − z 2 + 4
A. 2 3770 13
B. 10361 13
C. 3770 13
D. 10361 26
Cho hai số phức z 1 , z 2 thỏa mãn z 1 + 2 - 3 i và z 2 ¯ - 1 - 2 i = 1 Tìm giá trị lớn nhất của P = z 1 - z 2
A. P = 3 + 34
B. P = 3 + 10
C. P=6
D. P=3
Cho hai số phức z 1 , z 2 thỏa mãn z 1 − 3 = 2 và z 2 = iz 1 . Tìm giá trị nhỏ nhất của z 1 − z 2 .
A. 2 2
B. 2 − 1
C. 2
D. 2
Cho hai số phức z 1 ; z 2 thỏa mãn z 1 - 3 = 2 và z 2 = i z 1 . Tìm giá trị nhỏ nhất của z 1 - z 2
A. 2 2
B. 2
C. 2 - 1
D. 2
Cho 2 số phức z 1 và z 2 thỏa mãn: z 1 − 5 − i = 3 , z 2 + 5 − 2 i = iz 2 − 3 . Giá trị nhỏ nhất của biểu thức P = z 1 − z 2 là:
A. − 3 − 3 2 .
B. 3 + 3 2 .
C. 3 − 3 2 .
D. − 3 + 3 2 .