Chọn A.
Ta có: ![]()
Phương trình (*) là phương trình bậc hai ẩn 2x có: ![]()
Phương trình (*) có nghiệm 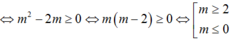
Áp dụng định lý Vi-ét ta có: ![]()
Do đó x1+ x2 = 3 khi 23 = 2m hay m = 4
Thử lại ta được m = 4 thỏa mãn.
Chọn A.
Ta có: ![]()
Phương trình (*) là phương trình bậc hai ẩn 2x có: ![]()
Phương trình (*) có nghiệm 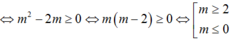
Áp dụng định lý Vi-ét ta có: ![]()
Do đó x1+ x2 = 3 khi 23 = 2m hay m = 4
Thử lại ta được m = 4 thỏa mãn.
Với giá trị nào của tham số m để phương trình 4 x - m . 2 x + 1 + 2 m + 3 = 0 có hai nghiệm x 1 , x 2 thỏa mãn x 1 + x 2 = 4
A. 5 2
B. 2
C. 8
D. 13 2
Với giá trị nào của tham số m để phương trình 4 x - m . 2 x + 1 + 2 m + 3 = 0 có hai nghiệm x 1 , x 2 thỏa mãn x 1 + x 2 = 4
A. m = 5 2
B. m = 2
C. m = 8
D. m = 13 2
Với giá trị nào của tham số m thì phương trình 4 x - m . 2 x + 1 + 2 m = 0 có hai nghiệm x 1 , x 2 thoả mãn x 1 + x 2 = 3
A.1
B.4
C.2
D.3
Với tất cả giá trị nào của tham số m thì phương trình ( m - 10 ) x 2 - 2 ( m - 2 ) x + m - 3 = 0 có hai nghiệm x 1 , x 2 thỏa mãn x 1 + x 2 + x 1 . x 2 < 1
A. 1<m<3.
B. 1<m<2.
C. m>2.
D. m>3.
Giá trị của tham số m để phương trình 4 x - m . 2 ( x + 1 ) + 2 m = 0 có 2 nghiệm x 1 , x 2 thỏa mãn x 1 + x 2 = 3 là
A. m = 2
B. m = 3
C. m = 1
D. m = 4
Cho phương trình 4 x - 2 x + 2 + m - 2 = 0 với m là tham số. Có tất cả bao nhiêu giá trị nguyên của m để phương trình đã cho có hai nghiệm phân biệt x 1 , x 2 thỏa mãn 0 ≤ x 1 < x 2
A.1
B.3
C.2
D.0
Biết m = m 0 là giá trị thực của tham số m sao cho phương trình 4 x - ( 4 m + 1 ) . 2 x + 2 4 m - 1 = 0 có hai nghiệm thực x 1 , x 2 thỏa mãn x 1 + 1 . x 2 + 1 = 6 . Khi đó m 0 thuộc khoảng nào sau đây?
![]()
![]()
![]()
![]()
Phương trình 4 x - m . 2 x + 1 + 2 m = 0 có hai nghiệm x 1 ; x 2 thỏa mãn x 1 + x 2 = 3 khi:
A. m=3
B. m=4
C. m=1
D. m=2
Phương trình 4 x - m . 2 x + 1 + 2 m = 0 có hai nghiệm x 1 , x 2 thỏa mãn x 1 + x 2 = 3 khi
A. 4
B. 3
C. 2
D. 1