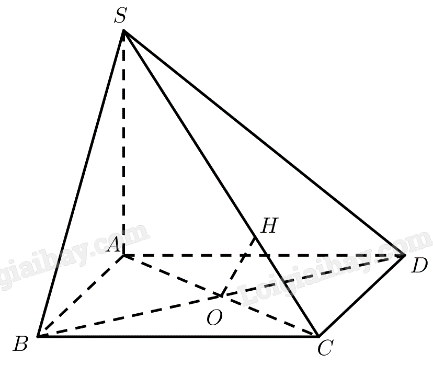
a) \(ABCD\) là hình vuông \( \Rightarrow BC\parallel A{\rm{D}}\)
Mà \(A{\rm{D}} \subset \left( {SA{\rm{D}}} \right)\)
\( \Rightarrow BC\parallel \left( {SAD} \right) \Rightarrow d\left( {BC,\left( {SAD} \right)} \right) = d\left( {B,\left( {SAD} \right)} \right)\)
\(SA \bot \left( {ABCD} \right) \Rightarrow SA \bot AB\)
\(ABCD\) là hình vuông \( \Rightarrow AB \bot A{\rm{D}}\)
\( \Rightarrow AB \bot \left( {SA{\rm{D}}} \right) \Rightarrow d\left( {B,\left( {SA{\rm{D}}} \right)} \right) = AB = a\)
Vậy \(d\left( {BC,\left( {SAD} \right)} \right) = a\).
b) \(ABCD\) là hình vuông \( \Rightarrow B{\rm{D}} \bot A{\rm{C}}\)
\(SA \bot \left( {ABCD} \right) \Rightarrow SA \bot B{\rm{D}}\)
\( \Rightarrow B{\rm{D}} \bot \left( {SAC} \right)\)
Gọi \(O = AC \cap B{\rm{D}}\), kẻ \(OH \bot SC\left( {H \in SC} \right)\)
\(B{\rm{D}} \bot \left( {SAC} \right) \Rightarrow B{\rm{D}} \bot OH\)
\( \Rightarrow d\left( {B{\rm{D}},SC} \right) = OH\)
\(\Delta ABC\) vuông tại \(B\)\( \Rightarrow AC = \sqrt {A{B^2} + B{C^2}} = a\sqrt 2 \Rightarrow OC = \frac{1}{2}AC = \frac{{a\sqrt 2 }}{2}\)
\(SA \bot \left( {ABCD} \right) \Rightarrow SA \bot AC \Rightarrow \Delta SAC\) vuông tại \(A\)\( \Rightarrow SC = \sqrt {S{A^2} + A{C^2}} = a\sqrt 3 \)
\(\Delta SAC \backsim \Delta OHC\,(g.g) \Rightarrow \frac{{SA}}{{OH}} = \frac{{SC}}{{OC}} \Rightarrow OH = \frac{{SA.OC}}{{SC}} = \frac{{a\sqrt 6 }}{6}\)
Vậy \(d\left( {B{\rm{D}},SC} \right) = \frac{{a\sqrt 6 }}{6}\).