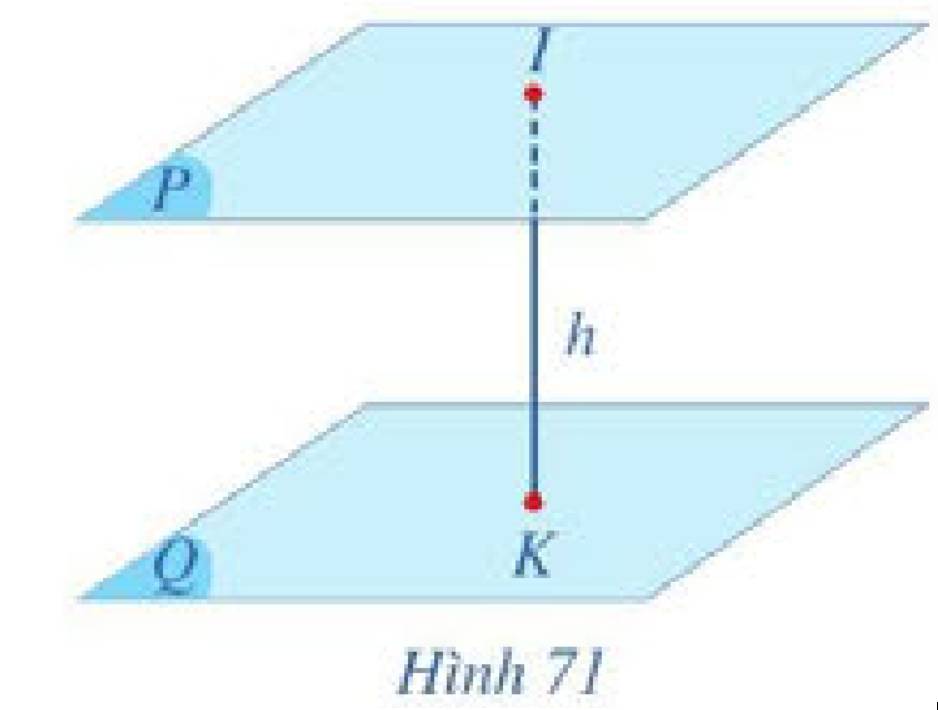
Kẻ \(SH\perp\left(ABC\right)\) \(\Rightarrow\widehat{SAH}=60^0\)
Áp dụng hệ thức lượng vào tam giác vuông có:
\(tan60^0=\dfrac{SH}{SA}\Leftrightarrow SH=\sqrt{3}a\)
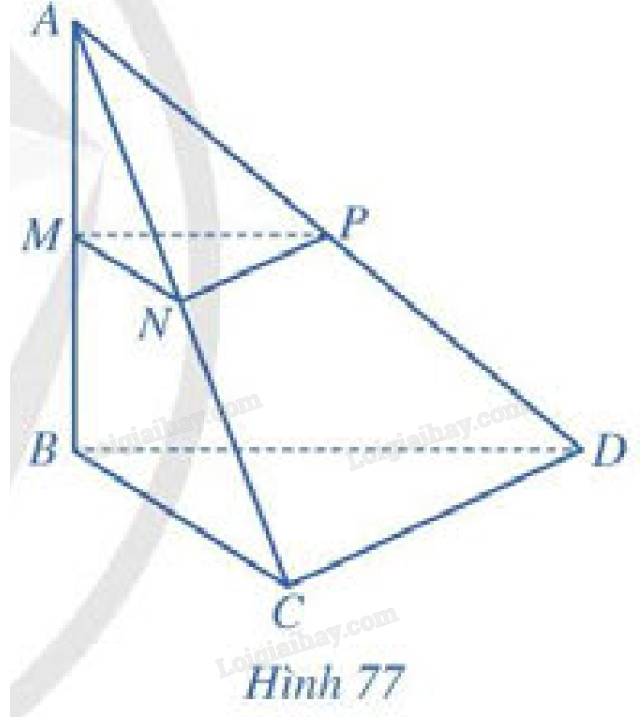
Ta có M và N lần lượt là trung điểm của SA và SB
\(\Rightarrow\) MN là đường trung bình của tam giác ABC
\(\Rightarrow MN//BC\)
mà \(BC\subset\left(ABC\right)\) , \(MN⊄(ABC) \)
\(\Rightarrow MN//\left(ABC\right)\)
\(d\left(MN,\left(ABC\right)\right)=d\left(M,\left(ABC\right)\right)=\dfrac{1}{2}d\left(S,\left(ABC\right)\right)=\dfrac{\sqrt{3}}{2}.a\)
Vậy \(d\left(MN,\left(ABC\right)\right)=\dfrac{\sqrt{3}}{2}a\)
Chứng minh \(d\left(M,\left(ABC\right)\right)=\dfrac{1}{2}d\left(S,\left(ABC\right)\right)\)
Kẻ \(MK\perp\left(ABC\right)\Rightarrow MK//SH\)
Áp dụng định lý thales: \(\dfrac{MK}{SH}=\dfrac{AM}{AS}=\dfrac{1}{2}\)
\(\Rightarrow MK=\dfrac{1}{2}SH\Rightarrow d\left(M,\left(ABC\right)\right)=\dfrac{1}{2}d\left(S,\left(ABC\right)\right)\) (đpcm)