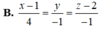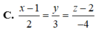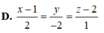Vectơ chỉ phương của đường thẳng d là \(\overrightarrow{v_d}\)=(1;1;2), \(\overrightarrow{AB}\)=(1;-1;0).
Vectơ chỉ phương của đường thẳng \(\Delta\) là \(\overrightarrow{v_{\Delta}}=\left[\left[\overrightarrow{AB},\overrightarrow{v_d}\right],\overrightarrow{v_d}\right]=-6\left(1;-1;0\right)\).
Phương trình đường thẳng cần tìm là \(\Delta\): \(\left\{{}\begin{matrix}x=1+t\\y=1-t\\z=1\end{matrix}\right.\).