Question

Vật trượt từ đỉnh mặt phẳng nghiêng nhãn dài l = 10m, góc nghiêng α = 30 ∘ . Hỏi vật tiếp tục chuyển động trên mặt phẳng ngang bao lâu khi xuống hết mặt phẳng nghiêng, biết hệ số ma sát với mặt phẳng ngang là μ = 0 , 1

A. 5s

B. 10s

C.  5 3 s

D.  10 3 s

Answer 1

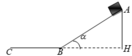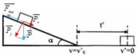
+ Gắn hệ trục tọa độ như hình vẽ

+ Viết phương trình định luật II – Niuton cho vật ta được:

P → + F m s → = m a → (1)

+ Chiếu (1) lên các phương ta được:

Ox:

P x − F m s = m a → a = P x − F m s m = P sin α − μ P cos α m = g sin α − μ g cos α

+ Vì mặt phẳng nghiêng nhẵn nên hệ số ma sát bằng 0, do đó:  a = g . sin α = 10. sin 30 0 = 5 m / s 2

+ Vận tốc của vật ở cuối mặt phẳng nghiêng là:  v = 2 a l = 2.5.10 = 10 m / s

+ Gia tốc của vật trên mặt phẳng ngang là:

a ' = − F m s m = − μ m g m = − μ g = − 0 , 1.10 = − 1 m / s 2

+ Thời gian vật đi trên mặt phẳng ngang là: t ' = v ' − v 0 ' a ' = 0 − v a '  (do vật dừng lại nên v′=0 )

Ta suy ra:  t ' = − v a ' = − 10 − 1 = 10 s

Đáp án: B