d)
Chu kỳ: \(T = \frac{2\pi}{\omega} = 1 \text{ giây}\)
Số lần vật đạt tốc độ:
\(\frac{v_{\text{max}}}{2}\) trong 1 chu kỳ: 4 lần
vậy số lần trong 5,25 giây:
\(5,25 \times 4 = 21 \text{ lần}\)
e)
Chu kỳ dao động:
\( T = \frac{2\pi}{\omega} = 1 \) giây ( trong 3,75 giây, vật thực hiện được 3 chu kỳ và 0,75 chu kỳ)
Quãng đường trong 3 chu kỳ đầu là: \( 12A = 60 \) cm
Quãng đường trong 0,75 chu kỳ tt là: \( 6A = 30 \) cm
Vậy quãng đường tổng cộng: \( S = 60 + 30 = 90 \) cm
Tốc độ trung bình:
\[
v_{\text{tb}} = \frac{S}{t} = \frac{90}{3,75} = 24 \, \text{cm/s}
\]
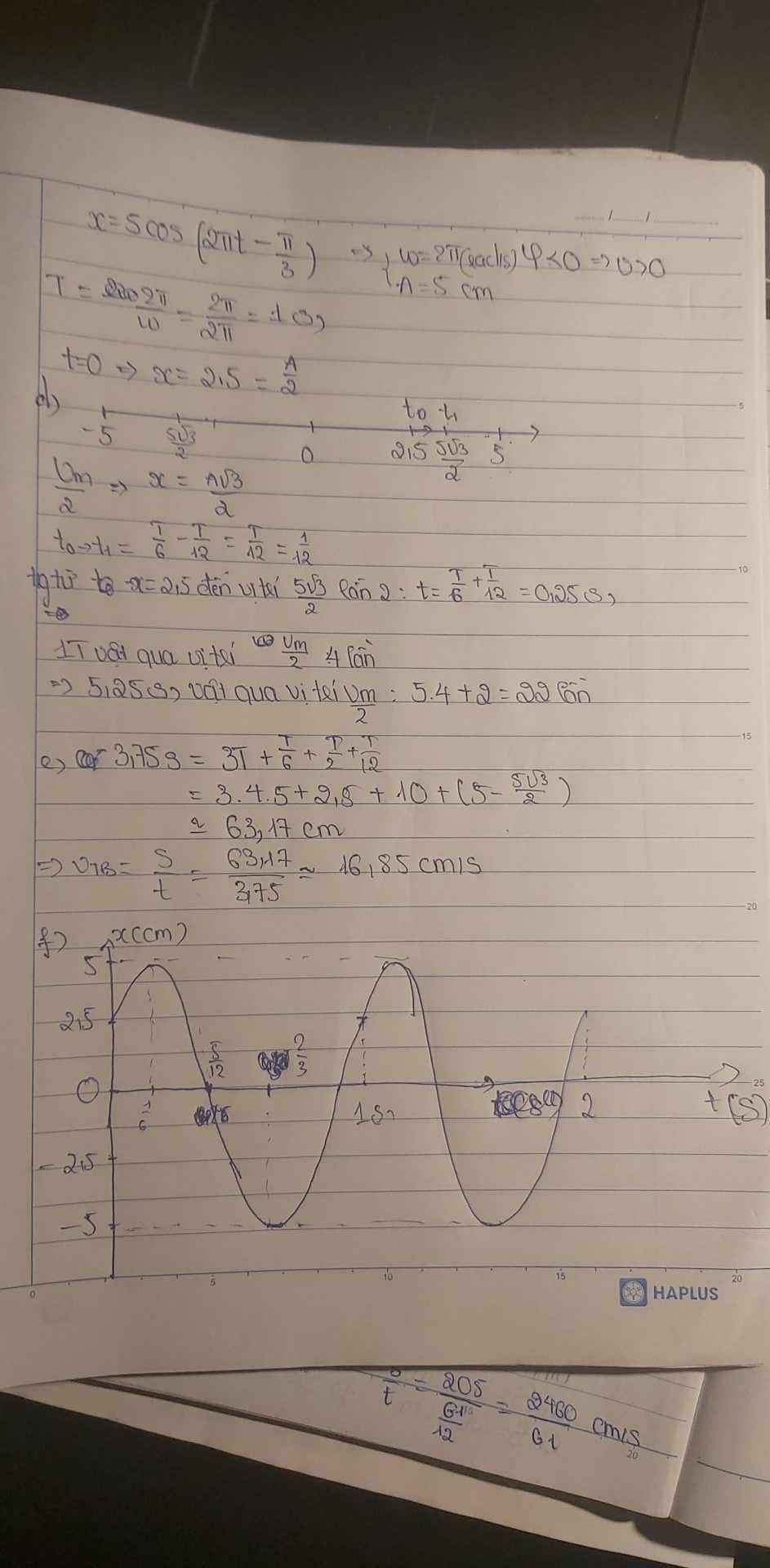
f) Vẽ đồ thị \((x, t)\) trong 2 chu kỳ đầu:
-> vẽ đồ thị dao động điều hòa dựa trên phương trình \(x = 5 \cos \left( 2\pi t - \frac{\pi}{3} \right)\) cho \(t\) từ 0 đến 2 giây
(bạn tự vẽ giúp mình ạ)