Lời giải:
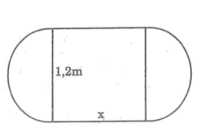
Gọi hcn đó có chiều dài và chiều rộng là $a,b$ (m)
Chu vi hcn: $2(a+b)=8\Rightarrow a+b=4$
Diện tích hcn: $S=ab\leq \left(\frac{a+b}{2}\right)^2=(\frac{4}{2})^2=4$ (theo BĐT AM-GM)
Vậy $S_{\max}=4$ khi $a=b=2$ (m)
Bán kính đường tròn ngoại tiếp hcn:
$R=\frac{\sqrt{a^2+b^2}}{2}=\frac{\sqrt{2^2+2^2}}{2}=\sqrt{2}$ (m)