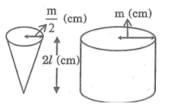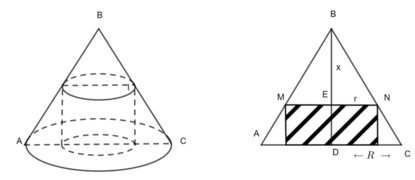
Gọi R là bán kính đáy ,h là chiều cao hình nón , r là bán kính đáy hình trụ x=BE là chiều cao phần hình nón bị cắt đi
Ta có: MN // AC

Phần bỏ đi của hình nón ít nhất tương đương với thể tích hình trụ là lớn nhất
Vì π,R,h là các hằng số nên thể tích hình trụ lớn nhất khi và chỉ khi x 2 (2h-2x) lớn nhất
Vì x + x + (2h -2x) =2h là một hằng số không đổi nên tích x.x(2h -2x) đạt giá trị lớn nhất khi
x = 2h – 2x ⇔ 3x =2h ⇒ 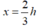
Vậy khi phần cắt bỏ ở phía trên hình nón có chiều cao bằng 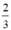 chiều cao hình nón thì phần bỏ đi là ít nhất
chiều cao hình nón thì phần bỏ đi là ít nhất


 A
.
2
π
3
(
c
m
3
)
B
.
4
π
3
(
c
m
3
)
C
.
2
π
(
c
m
3
)
D
.
8
π
3
(
c
m
3
)
A
.
2
π
3
(
c
m
3
)
B
.
4
π
3
(
c
m
3
)
C
.
2
π
(
c
m
3
)
D
.
8
π
3
(
c
m
3
)