Lời giải:
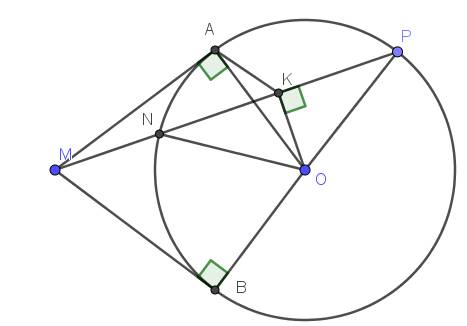
Vì $MA,MB$ là tiếp tuyến của $O$ nên $MA\perp OA, MB\perp OB$
$\Rightarrow \widehat{MAO}=\widehat{MBO}=90^0$
Xét tứ giác $MAOB$ có $\widehat{MAO}+\widehat{MBO}=90^0+90^0=180^0$. Mà 2 góc này đối nhau nên $MAOB$ là tứ giác nội tiếp.
$\Rightarrow M, A,O,B$ cùng thuộc 1 đường tròn (1)
Mặt khác:
Tam giác $ONP$ cân tại $O$ (do $ON=OP=R$) nên trung tuyến $OK$ đồng thời là đường cao.
$\Rightarrow \widehat{MKO}=90^0$
Xét tứ giác $MAKO$ có $\widehat{MAO}=\widehat{MKO}=90^0$. Mà 2 góc này cùng nhìn cạnh $MO$ nên $MAKO$ là tứ giác nội tiếp.
$\Rightarrow M,A,K,O$ cùng thuộc 1 đường tròn (2)
Từ $(1); (2)\Rightarrow M, A, O, K,B$ cùng thuộc 1 đường tròn.