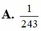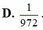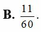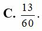Đáp án B
Phương pháp: Xét các trường hợp:
TH1: a1 + a2 = a3 + a4 = a5 + a6 = 5
TH2: a1 + a2 = a3 + a4 = a5 + a6 = 6
TH3: a1 + a2 = a3 + a4 = a5 + a6 = 7
Cách giải:
TH1: a1 + a2 = a3 + a4 = a5 + a6 = 5, ta có 0 + 5 = 1 + 4 = 2 + 3
- Nếu (a1;a2) = (0;5) => có 1 cách chọn (a1a2)
Có 2 cách chọn (a3a4), 2 số này có thể đổi vị trí cho nhau nên có 4 cách chọn.
Tương tự (a5a6) có 2 cách chọn.
=> Có 8 số thỏa mãn.
- Nếu (a1;a2) ↓ (0;5) => có 2 cách chọn (a1a2), 2 số này có thể đổi vị trí cho nhau nên có 4 cách chọn.
Có 2 cách chọn (a3a4), 2 số này có thể đổi vị trí cho nhau nên có 4 cách chọn.
Tương tự (a5a6) có 2 cách chọn.
=> Có 32 số thỏa mãn.
Vậy TH1 có: 8 + 32 = 40 số thỏa mãn.
TH2: a1 + a2 = a3 + a4 = a5 + a6 = 6, ta có 0 + 6 = 1 + 5 = 2 + 4 = 6.
Tương tự như TH1 có 40 số thỏa mãn.
TH3: a1 + a2 = a3 + a4 = a5 + a6 = 7, ta có 1 + 6 = 2 + 5 = 3 + 4 = 7
Có 3 cách chọn (a1a2), hai số này có thể đổi chỗ cho nhau nên có 6 cách chọn.
Tương tự có 4 cách chọn (a3a4) và 2 cách chọn (a5a6).
Vậy TH3 có 6.4.2 = 48 số thỏa mãn.
Vậy có tất cả 40 + 40 + 48 = 128 số có 6 chữ số khác nhau thỏa mãn a1 + a2 = a3 + a4 = a5 + a6
Để viết một số có 6 chữ số khác nhau bất kì có 6.6.5.4.3.2 = 4320 số.
Vậy P = 128 4320 = 4 135 .