Trước kỳ thi học kỳ 2 của lớp 11 tại trường FIVE, giáo viên Toán lớp FIVA giao cho học sinh để cương ôn tập gồm 2n bài toán, n là số nguyên dương lớn hơn 1. Đề thi học kỳ của lớp FIVA sẽ gồm 3 bài toán được chọn ngẫu nhiên trong số 2n bài toán đó. Một học sinh muốn không phải thi lại, sẽ phải làm được ít nhất 2 trong số 3 bài toán đó. Học sinh TWO chỉ giải chính xác được đúng 1 nửa số bài trong đề cương trước khi đi thi, nửa còn lại học sinh đó không thể giải được. Tính xác suất để TWO không phải thi lại ?
A. c
B. 1 2
C. 3 4
D. 1 3
Đáp án B
Phương pháp : Chia hai trường hợp :
TH1 : Học sinh TWO làm được 2 trong số 3 bài trong đề thi.
TH2 : Học sinh TWO làm được cả 3 bài trong đề thi.
Cách giải : Ω = C 2 n 3
TH1 : Học sinh TWO làm được 2 trong số 3 bài trong đề thi. Có C n 2 . C n 1 cách
TH2 : Học sinh TWO làm được cả 3 bài trong đề thi. Có C n 3 cách
Gọi A là biến cố học sinh TWO không phải thi lại
![]()
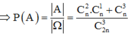
Đến đây chọn một giá trị bất kì của n rồi thay vào là nhanh nhất, chọn n =10 , ta tính được P ( A ) = 1 2

