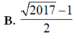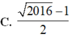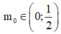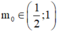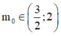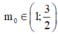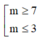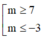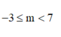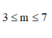Đáp án D
Phương pháp
Biện luận để tìm trực tiếp nghiệm z 1 , z 2 . Sử dụng giả thiết để tìm ra giá trị m 0
Lời giải chi tiết.
Viết lại phương trình đã cho thành ![]()
Nếu m 0 = 9 ⇒ z = 3 Hay phương trình chỉ có một nghiệm. (Loại)
Nếu
m
0
<
9
thì phương trình đã cho có hai nghiệm thực ![]()

Nếu m 0 > 9 thì phương trình đã cho có hai nghiệm phức liên hợp là
![]()
Khi đó ![]()
Do đó m 0 > 9 thỏa mãn yêu cầu bài toán.
Do bài toán đòi hỏi
m
0
∈
(
0
;
20
)
nên ![]()
Vậy có 10 giá trị thỏa mãn.