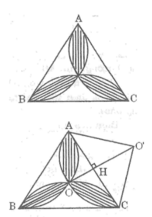
Gọi O là tâm của tam giác đều ABC
Ta có: OA =OB=OC
Vì ABC là tam giác đều nên AO,BO , CO là tia phân giác của góc A , góc B ,góc C trong ∆ OAC ta có:

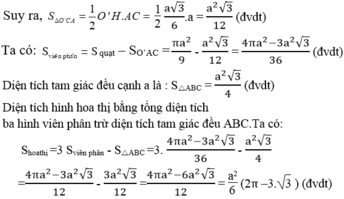

Gọi O là tâm của tam giác đều ABC
Ta có: OA =OB=OC
Vì ABC là tam giác đều nên AO,BO , CO là tia phân giác của góc A , góc B ,góc C trong ∆ OAC ta có:

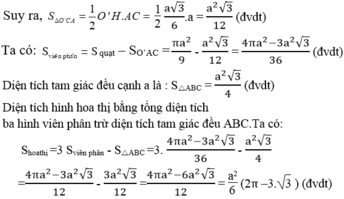
a) Vẽ lại hình tạo bởi các cung tròn xuất phát từ đỉnh C của tam giác đều ABC cạnh 1cm. Nêu cách vẽ (h.63).
b) Tính diện tích miền gạch sọc.
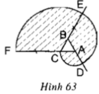
Cho tam giác đều ABC. Gọi O là tâm của đường tròn đi qua đỉnh A, B, C.
Tính số đo các cung tạo bởi hai trong ba điểm A, B, C.
Cho tam giác ABC cân tại A, hình vuông KLMN có đỉnh K trên cạnh AB, đỉnh L trên cạnh AC, các đỉnh M,N ở trên đáy BC
a) Tính tỉ số diện tích của tam giác và hình vuông khi tâm hình vuông trùng với trọng tâm tam giác
b) Tính cạnh hình vuông biết BC=16 ; AB=20
tính góc A của tam giác ABC sao cho đỉnh B cách đều tâm đường tròn bằng tiếp tam giác tại đỉnh A và B
Câu 1: Một hình vuông và 1 tam giác đều cùng nội tiếp trong một đường tròn (O;1) sao cho một cạnh của tam giác song song với một cạnh của hình vuông. tính diện tích phần chung của tam giác và hình vuông.
Câu 2: Cho tứ giác ABCD nội tiếp dường tròn tâm O. Cho biết phân giác của các góc BAD và ABC cắt nhau tại một điểm E trên CD.
a> Cm: AD+BC=CD
B> Cho biết CD/CB=k>1 tính S ADE/ S BCE
cho tam giác ABC biết các đường trung tuyến xuất phát tại các đỉnh A và B lần lượt bằng 3cm, 3,6cm; cạnh BC=4cm. tính diện tích tam giác ABC và tính hai cạnh còn lại của tam giác ABC
1. cho nữa đường tròn tâm O bán kính R có đường kính AB và bán kính AC vuông góc AB, điểm M di động trên cung AC, điểm H là hình chiếu của M lên OC. xác dịnh vị trí của M để MA + MH lớn nhất
2. cho (o;r) có đường kính AB, đường trung trực của AO cắt đường tròn ở C và D.
a. tứ giác ACOD là hình j
b. tam giác BCD là tam giác j
c. tính chu vi và diện tích tam giác BCD
3. tam giác ABC nhọn nội tiếp đường tròn O; AB là 1 đường kính của đường tròn. H là trực tâm của tam giác ABC.
a. CM: tứ giác BHCD là hình bình hành
b. CM: HA + HB + HC = 2( OM + ON + OK) trong đó M, N, K là hình chiếu của O lên 3 cạnh của tam giác ABCgiúp với1. cho nữa đường tròn tâm O bán kính R có đường kính AB và bán kính AC vuông góc AB, điểm M di động trên cung AC, điểm H là hình chiếu của M lên OC. xác dịnh vị trí của M để MA + MH lớn nhất
2. cho (o;r) có đường kính AB, đường trung trực của AO cắt đường tròn ở C và D.
a. tứ giác ACOD là hình j
b. tam giác BCD là tam giác j
c. tính chu vi và diện tích tam giác BCD
3. tam giác ABC nhọn nội tiếp đường tròn O; AB là 1 đường kính của đường tròn. H là trực tâm của tam giác ABC.
a. CM: tứ giác BHCD là hình bình hành
b. CM: HA + HB + HC = 2( OM + ON + OK) trong đó M, N, K là hình chiếu của O lên 3 cạnh của tam giác ABCgiúp với
Một đường thẳng đi qua đỉnh A của tam giác ABC cắt cạnh BC tại K và cắt đường trung tuyến BM tại I sao cho BI:IM=1:2. Tính tỉ số diện tích tam giác ABK và tam giác ABC
Cho tam giác ABC có ba góc đều nhọn nội tiếp đường tròn tâm O, các đường cao BM,CN của tam giác cắt nhau tại H. Cho cạnh BC cô định, A thay đổi trên cung lớn BC sao cho tam giác ABC luôn nhọn. Xác định vị trí điể A để diện tích tam giác BCH lớn nhất