Trong mặt phẳng với hệ toạ độ Oxy cho tam giác ABC. Hai điểm M 4 ; - 1 , N 0 ; - 5 lần lượt thuộc AB, AC và phương trình đường phân giác trong góc A là x - 3 y + 5 = 0 , trọng tâm của tam giác ABC là G. Tìm toạ độ các đỉnh của tam giác ABC
A. A 1 ; 2 , B - 2 ; 5 , C - 1 ; 12
B. A 1 ; 2 , B - 2 ; 5 , C 0 ; 1
C. A 1 ; 0 , B - 2 ; 5 , C - 1 ; 12
D. A 1 ; 2 , B - 1 ; 5 , C - 1 ; 12
Đáp án A
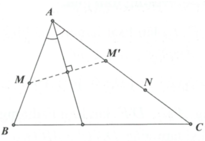
Phân tích.
- Ta thấy A thuộc đường phân giác trong góc A: x - 3 y + 5 = 0 giờ chỉ cần viết được phương trình AC là tìm được A.
- Trên AC đã có một điểm N, cần tìm thêm một điểm nữa. Chú ý khi lấy M’ đối xứng với M qua phân giác trong ta có M’ thuộc cạnh AC.
- Tìm M’ viết được phương trình AC từ đó suy ra A. Có A, M viết được phương trình AB.
- Gọi B, C và tham số hóa dựa vào B thuộc AB, C thuộc AC. Áp dụng công thức trọng tâm sẽ tìm ra được tọa độ B, C.
Hướng dẫn giải.
Gọi M ' ∈ A C là điểm đối xứng của M qua phân giác trong góc A, gọi I là giao điểm của MM' với phân giác trong góc A → I là trung điểm MM’.
Phương trình MM’ là: 3 x + y - 11 = 0
Toạ độ điểm I là nghiệm của hệ:
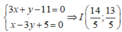
M’ đối xứng với M qua
![]()
Đường thẳng AC qua N và M’ nên có phương trình:
![]()
Tọa độ A là nghiệm của hệ:
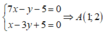
Đường thẳng AB đi qua A, M nên có phương trình:
x + y - 3 = 0
Gọi
![]()
Do G là trọng tâm tam giác ABC nên ta có:
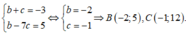
Vậy tọa độ các đỉnh của tam giác ABC là:
![]()

