Các câu hỏi tương tự
Trong mặt phăng Oxy, cho phép biến hình f xác định như sau. Với mỗi M (x; y), ta có M f (M) sao cho M(x;y) thỏa mãn x x, y ax + by, với a, b là các hằng số thực. Khi đó a và b nhận giá trị nào trong các giá trị sau đây thì f trở thành phép biến hình đồng nhất?
Đọc tiếp
Trong mặt phăng Oxy, cho phép biến hình f xác định như sau. Với mỗi M (x; y), ta có M' = f (M) sao cho M'(x';y') thỏa mãn x' = x, y' = ax + by, với a, b là các hằng số thực. Khi đó a và b nhận giá trị nào trong các giá trị sau đây thì f trở thành phép biến hình đồng nhất?
![]()
![]()
![]()
![]()
Trong mặt phẳng tọa độ Oxy, biết điểm M’(-3;0) là ảnh của điểm M(1;-2) qua phép tịnh tiến theo vectơ
u
→
và M”(2;3) là ảnh của điểm M’ qua phép tịnh tiến theo vectơ
v
→
. Tìm tọa độ vectơ
u
→
+
v
→
. A. (1;5) B. (-4;2) C. (5;3) D. (0;1)
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, biết điểm M’(-3;0) là ảnh của điểm M(1;-2) qua phép tịnh tiến theo vectơ u → và M”(2;3) là ảnh của điểm M’ qua phép tịnh tiến theo vectơ v → . Tìm tọa độ vectơ u → + v → .
A. (1;5)
B. (-4;2)
C. (5;3)
D. (0;1)
Trong mặt phằng tọa độ Oxy, cho điểm M’(4;2) Biết M’ là ảnh của M qua phép tịnh tiến theo vec tơ
v
→
1
;
5
.
Tìm tọa độ của điểm M A.
M
−
3
;
−
5
.
B.
M
3
;
7...
Đọc tiếp
Trong mặt phằng tọa độ Oxy, cho điểm M’(4;2) Biết M’ là ảnh của M qua phép tịnh tiến theo vec tơ v → 1 ; 5 . Tìm tọa độ của điểm M
A. M − 3 ; − 5 .
B. M 3 ; 7 .
C. M − 5 ; 7 .
D. M − 5 ; − 3 .
Trong không gian Oxyz cho mặt phẳng (α) có phương trình 4x + y + 2z + 1 =0 và mặt phẳng ( β) có phương trình 2x – 2y + z + 3 = 0
Tìm điểm M' là ảnh của M(4; 2; 1) qua phép đối xứng qua mặt phẳng (α).
Cho tam giác ABCcó trọng tâm G. Gọi M, N, P lần lượt là trung điểm của các cạnh AB, BC, CA. Phép vị tự nào sau đây biến tam giác ABC thành tam giác NPM A.
V
A
;
−
1
2
.
B.
V
G
;
1
2...
Đọc tiếp
Cho tam giác ABCcó trọng tâm G. Gọi M, N, P lần lượt là trung điểm của các cạnh AB, BC, CA. Phép vị tự nào sau đây biến tam giác ABC thành tam giác NPM
A. V A ; − 1 2 .
B. V G ; 1 2 .
C. V G ; − 2 .
D. V G ; − 1 2 .
trong phép toán 2 ngôi, hãy kiểm tra tính kết hợp, giao hoán và tìm phần tử đơn vị nếu có :
a/ tập số hữu tỉ Q với phép toán a^b=1/2 ab
b/ Tập số tự nhiên N với phép toán m^n=max(m,n)
c/ Tập số thực R với phép toán a o b =a+b-ab
Cho điểm M ( 3 ; 2 ; - 1 ) , điểm đối xứng của M qua mặt phẳng (Oxy) là điểm
A. M'(3;-2;1)
B. M'(3;-2;-1)
C. M'(3;2;1)
D. M'(3;2;0)
Trong mặt phẳng tọa độ Oxy, cho các điểm A(1;-1), A’(2;0) và B(0;1), B’(-2;1). Phép quay tâm I(a;b) biến A thành A' và biến B thành B'. Tính P=a.b
A. -2
B. 1
C. 4
D. 3
Cho điểm M (1; 2; 5), mặt phẳng (P) đi qua điểm M cắt trục tọa độ Ox; Oy; Oz tại A, B, C sao cho M là trực tâm của tam giác ABC. Phương trình mặt phẳng (P) là
Đọc tiếp
Cho điểm M (1; 2; 5), mặt phẳng (P) đi qua điểm M cắt trục tọa độ Ox; Oy; Oz tại A, B, C sao cho M là trực tâm của tam giác ABC. Phương trình mặt phẳng (P) là
![]()
![]()
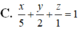
![]()