Lời giải:
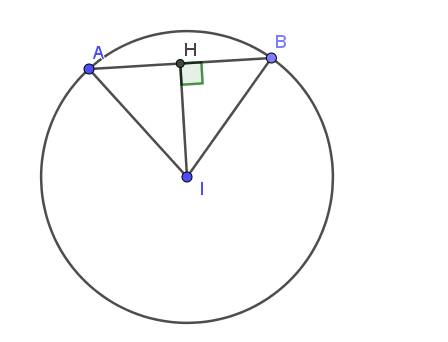
Từ $I$ kẻ $IH\perp AB$ thì $H$ là trung điểm $AB$
$\Rightarrow IH = AB:2 =10:2=5$
$IH = d(I, AB) = \frac{|4x_I-3y_I-3|}{\sqrt{4^2+(-3)^2}}=\frac{|4(-4)-3.2-3|}{5}=5$
Áp dụng định lý Pitago:
$R^2=IA^2=IH^2+AH^2=5^2+5^2=50$
Vậy phương trình đường tròn cần tìm là:
$(x+4)^2+(y-2)^2=50$