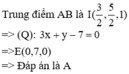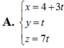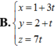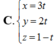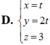Trong không gian với trục tọa độ Oxyz, cho hai điểm A 3 ; 3 ; 1 , B 0 ; 2 ; 1 và mặt phẳng P : x + y + z - 7 = 0 . Đường thẳng d nằm trong P sao cho mọi điểm nằm trên d luôn cách đều A, B có phương trình là.
A. d : x - 1 = y - 7 3 = z - 2
B. d : x - 1 1 = y - 7 3 = z 2
C. d : x - 1 = y + 7 3 = z - 2
D. d : x + 1 1 = y - 7 3 = z - 4 2
Chọn A
Gọi (Q) là mặt phẳng trung trực của đoạn thẳng AB
=> Mọi điểm thuộc (Q) đều cách đều AB
Để mọi điểm nằm trên d đều cách đều AB thì d phải thuộc Q
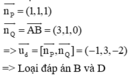
Đường thẳng d nằm trong cả (P) và (Q) => d phải đi qua 1 điểm nằm trong cả (P) và (Q)
Gọi điểm chung này là E