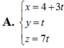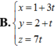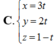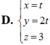Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng (P) có phương trình 1 - m 2 2 n . x + 4 m n . y + 1 + m 2 1 - n 2 . z + 4 m 2 n 2 + m 2 + n 2 + 1 = 0 , với m, n là tham số thực tùy ý. Biết rằng mặt phẳng (P) luôn tiếp xúc với một mặt cầu cố định khi m, n thay đổi. Tìm bán kính mặt cầu đó?
A. 1
B. 2
C. 3
D. 4
Đáp án D.
Gọi I(a,b,c) là tâm mặt cầu cố định đó. Rõ ràng d(I,(P)) = R không đối với mọi m , n ∈ ℝ .
Với m = 1 ⇒ d I , P = 2 n b + 1 - n 2 c + 4 n 2 + 1 4 n 2 + 1 - n 2 2 = R
Với m = - 1 ⇒ d I , P = - 2 n b + 1 - n 2 c + 4 n 2 + 1 4 n 2 + 1 - n 2 2 = R
⇒ 2 n b + 1 - n 2 c + 4 n 2 + 1 = - 2 n b + 1 - n 2 c + 4 n 2 + 1 ⇔ [ b = 0 1 - n 2 c + 4 n 2 + 1 = 0
Rõ ràng 1 - n 2 c + 4 n 2 + 1 = 0 không thể xảy ra với mọi n ∈ ℝ suy ra b = 0
Với m = n = 1 ⇒ d I , P = b + 4 = R = 4 .