Chọn đáp án C
Mặt phẳng (P) có vectơ pháp tuyến là n 1 ⇀ = 2 ; a ; 3 ; mặt phẳng (Q) có vectơ pháp tuyến là n 2 ⇀ = b ; - 6 ; - 6 .
Để (P)//(Q) thì n 1 ⇀ , n 2 ⇀ cùng phương hay n 1 ⇀ = k n 2 ⇀
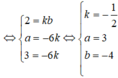
Chọn đáp án C
Mặt phẳng (P) có vectơ pháp tuyến là n 1 ⇀ = 2 ; a ; 3 ; mặt phẳng (Q) có vectơ pháp tuyến là n 2 ⇀ = b ; - 6 ; - 6 .
Để (P)//(Q) thì n 1 ⇀ , n 2 ⇀ cùng phương hay n 1 ⇀ = k n 2 ⇀
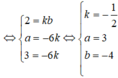
Trong không gian với hệ tọa độ Oxyz có bao nhiêu mặt phẳng song song với mặt phẳng (Q): x + y + z + 3 = 0 cách điểm M(3;2;1) một khoảng bằng 3 3 biết rằng tồn tại một điểm X(a,b,c) trên mặt phẳng đó thỏa mãn a + b + c < –2?
A. 2
B. 1
C. Vô số
D. 0
Trong không gian với hệ tọa độ Oxyz có bao nhiêu mặt phẳng song song với mặt phẳng Q : x + y + z + 3 = 0 , cách điểm M(3;2;1) một khoảng bằng 3 3 biết rằng tồn tại một điểm X(a;b;c) trên mặt phẳng đó thỏa mãn a + b + c < − 2 ?
A. 1
B. Vô số
C. 2
D. 0
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A (1;-2;-3); B(1;1;1) và hai đường thẳng ∆ 1 : x - 2 1 = y - 2 4 = z + 6 - 3 ; ∆ 2 : x - 2 1 = y + 3 - 4 = z - 4 3 . Gọi m là số mặt phẳng (P) tiếp xúc với mặt cầu đường kính AB đồng thời song song với cả hai đường thẳng ∆1;∆2; n là số mặt phẳng (Q), sao cho khoảng cách từ A đến (Q) bằng 15, khoảng cách từ B đến (Q) bằng 10. Chọn mệnh đề đúng trong các mệnh đề sau.
A. m + n = 1
B. m + n = 4
C. m + n = 3
D. m + n = 2
Trong không gian với hệ trục tọa độ Oxyz, cho ba điểm A(0;-2;-l), B(-2;-4;3), C(l;3;-l) và mặt phẳng P : x + y - 2 z - 3 = 0 . Tìm điểm M ∈ P sao cho M A → + M B → + 2 M C → đạt giá trị nhỏ nhất.
A. M 1 2 ; 1 2 ; - 1
B. M - 1 2 ; - 1 2 ; 1
C. M(2;2;-4)
D. (-2;-2;4)
Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng (P): x+y+z-2=0, (Q): x+2y-z+3=0 và điểm A(1;0;4). Phương trình đường thẳng qua A và cùng song song với (P) và (Q) là:
A. d : x - 1 - 3 = y 2 = z - 4 1
B. d : x - 1 3 = y 1 = z - 4 1
C. d : x - 1 - 3 = y - 1 = z - 4 1
D. d : x - 1 - 3 = y 2 = z - 4 - 1
Trong không gian với hệ trục tọa độ Oxyz cho A (1; 2; ‒1), B (‒2; 1; 0). Điểm M a ; b ; c thuộc mặt phẳng P : x - 2 y + z + 4 = 0 sao cho M A = M B = 11 2 . Khi đó giá trị của a bằng?
A. a = ± 1 2
B. a = 11 4
C. a = 1 2
D. a = - 1 2
Trong không gian với hệ trục tọa độ Oxyz cho 3 điểm A(1;1;1). B(0;1;2), C(-2;1;4) và mặt phẳng ( P ) : x - y + z + 2 = 0 . Tìm điểm NÎ(P) sao cho S = 2 N A 2 + N B 2 + N C 2 đạt giá trị nhỏ nhất
A. N - 4 3 ; 2 ; 4 3
B. N(-2;0;1).
C. N - 1 2 ; 5 4 ; 3 4
D. N(-1;2;1)
Trong không gian với hệ trục tọa độ Oxyz, cho hai đường thẳng a : x 1 = y 1 = z - 2 ; b : x + 1 - 2 = y 2 = z + 1 - 1 và mặt phẳng ( P ) : x - y - z = 0 . Viết phương trình của đường thẳng d song song với (P), cắt a và b lần lượt tại M và N mà M N = 2 .
A. d : 7 x - 4 3 = 7 y + 4 8 = 7 z + 8 - 5
B. d : 7 x + 4 3 = 7 y - 4 8 = 7 z + 8 - 5 .
C. d : 7 x - 1 3 = 7 y - 4 8 = 7 z + 3 - 5
D. d : 7 x - 1 3 = 7 y + 4 8 = 7 z + 8 - 5
Trong không gian với hệ trục tọa độ Oxyz, cho các điểm A ( a ; 0 ; 0 ) , B ( 0 ; b ; 0 ) , C ( 0 ; 0 ; c ) , trong đó a > 0 , b > 0 , c > 0 và 3 a + 1 b + 3 c = 5 . Biết mặt phẳng (ABC) tiếp xúc với mặt cầu (S) có phương trình là ( x - 3 ) 2 + ( y - 1 ) 2 + ( z - 3 ) 2 = 304 25 , khi đó thể tích của khối tứ diện OABC nằm trong khoảng nào?
A . ( 0 ; 1 2 ) .
B. (0;1).
C. (1;3).
D. (4;5).