Giả sử đường phân giác trong của góc A cắt cạnh BC tại D.
Ta có
![]()
phương trình BC là:
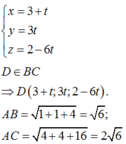
Áp dụng tính chất đường phân giác ta có:
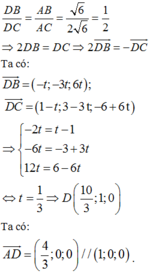
Vậy phương trình đường thẳng
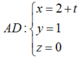
Chọn C.
Giả sử đường phân giác trong của góc A cắt cạnh BC tại D.
Ta có
![]()
phương trình BC là:
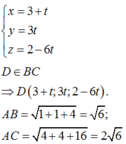
Áp dụng tính chất đường phân giác ta có:
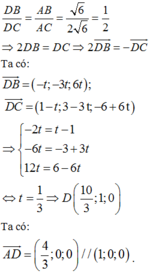
Vậy phương trình đường thẳng
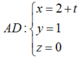
Chọn C.
Trong không gian với hệ tọa độ Oxyz cho tam giác ABC vuông tại C có A B C ^ = 60 ° ; A B = 3 2 . Đường thẳng AB có phương trình x - 3 1 = y - 4 1 = x + 8 - 4 , đường thẳng AC nằm trên mặt phẳng α : x + z - 1 = 0 . Biết điểm B là điểm có hoành độ dương, gọi (a,b,c) là tọa độ của điểm C. Giá trị a + b + c bằng
A. 2
B. 3
C. 4
D. 7
Trong không gian với hệ toạ độ oxyz, cho A(1 ;-2 ;1),B(-2 ;2 ;1),C(1,-2,2) Đường phân giác trong góc A của tam giác ABC cắt mặt phẳng (P) : x+y+z-6=0 tại điểm nào trong các điểm sau đây
A. (-2 ;3 ;5)
B. (-2 ;2 ;6)
C. (1 ;-2 ;7)
D. (4 ;-6 ;8)
Trong không gian Oxyz, cho tam giác ABC với A(2;3;3), đường trung tuyến kẻ từ đỉnh B là x - 3 - 1 = y - 3 2 = z - 2 - 1 , phương trình đường phân giác trong góc C là x - 2 2 = y - 4 - 1 = z - 2 - 1 . Đường thẳng AB có một véctơ chỉ phương là
A. u 1 → 0 ; 1 ; - 1
B. u 2 → 2 ; 1 ; - 1
C. u 3 → 1 ; 2 ; 1
D. u 4 → 1 ; - 1 ; 0
Trong không gian Oxyz, cho tam giác ABC có A(2;3;3), phương trình đường trung tuyến kẻ từ B là x - 3 - 1 = y - 3 2 = z - 2 - 1 , phương trình đường phân giác trong của góc C là x - 2 2 = y - 4 - 1 = z - 2 - 1 . Đường thẳng BC có một vectơ chỉ phương là
A. u → = 2 ; 1 ; - 1
B. u → = 1 ; 1 ; 0
C. u → = 1 ; - 1 ; 0
D. u → = 1 ; 2 ; 1
Trong không gian Oxyz, cho tam giác ABC có A ( 2;3;3) phương trình đường trung tuyến kẻ từ B là x − 3 − 1 = y − 3 2 = z − 2 − 1 , phương trình đường phân giác trong của góc C là x − 2 2 = y − 4 − 1 = z − 2 − 1 . Đường thẳng AB có vecto chỉ phương là :
A. u 3 → 2 ; 1 ; − 2
B. u 2 → 1 ; − 1 ; 0
C. u 4 → 0 ; 1 ; − 1
D. u 1 → 1 ; 2 ; 1
Trong không gian Oxyz cho tam giác ABC có A ( 2;3;3) phương trình đường trung tuyến kẻ từ B là x − 3 − 1 = y − 3 2 = z − 2 − 1 , phương trình đường phân giác trong của góc C là x − 2 2 = y − 4 − 1 = z − 2 − 1 . Biết rằng u → = m ; n ; − 1 là một véc tơ chỉ phương của đường thẳng AB. Tính giá trị của biểu thức T = m 2 + n 2
A. T = 1
B. T = 5
C. T = 2
D. T = 10
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d : x - 2 1 = y + 1 1 = z + 1 2 và ∆ : x - 3 1 = y + 1 1 = z + 3 2 . Viết phương trình mặt phẳng (P) chứa d và tạo với tam giác một góc 30 ° . có dạng x + ay + bz + c = 0 với a , b , c , ∈ ℤ khi đó giá trị a + b + c là
A. 8
B. -8
C. 7
D. -7
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d: x - 2 1 = y - 2 2 = z + 2 - 1 và mặt phẳng ( α ) :2x+2y-z-4=0. Tam giác ABC có A(-1;2;1), các đỉnh B, C nằm trên (α) và trọng tâm G nằm trên đường thẳng d. Tọa độ trung điểm M của BC là
A. M(2;1;2)
B. M(0;1;-2)
C. M(1;-1;-4)
D. M(2;-1;-2)
Trong hệ trục tọa độ Oxyz, cho tam giác ABC có C(3;2;3), đường cao AH nằm trên đường thẳng d 1 : x - 2 1 = y - 3 1 = z - 3 - 2 và đường phân giác trong BD của góc B nằm trên đường thẳng d2 có phương trình x - 1 1 = y - 4 - 2 = z - 3 1 . Diện tích tam giác ABC bằng
A. 4
B. 2 3
C. 4 3
D. 8