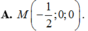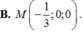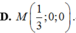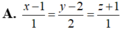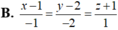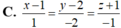Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng ( α ) : x + y + z - 4 = 0 mặt cầu ( S ) : x 2 + y 2 + z 2 - 8 x - 6 y - 6 z + 18 = 2 và điểm M(1;1;2) ∈ ( α ) . Đường thẳng d đi qua M nằm trong mặt phẳng ( α ) và cắt mặt cầu (S) tại hai điểm phân biệt A, B sao cho dây cung AB có đọ dài nhỏ nhất. Đường thẳng d có một véc tơ chỉ phương là
A. u 1 → = ( 2 ; - 1 ; - 1 )
B. u 3 → = ( 1 ; 1 ; - 2 )
C. u 2 → = ( 1 ; - 2 ; 1 )
D. u 4 → = ( 0 ; 1 ; - 1 )
Đáp án C
![]()
có tâm I(4;3;3) bán kính R =4
Gọi phương trình đường thẳng d có dạng
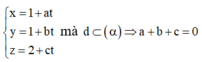
Khoảng cách từ tâm I đến d là
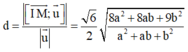
Ta có
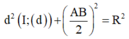
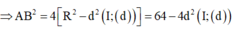
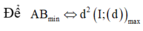
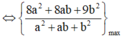
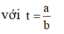
Khi đó

![]()