Đáp án B
Mặt phẳng trung trực của MN nhận 
làm véc-tơ pháp tuyến và đi qua trung điểm I(2;0;-1) của MN nên nó có phương trình x+y-3z-5=0.
Trong không gian Oxyz, mặt phẳng qua A(1;2;-1) và vuông góc với các mặt phẳng (P): 2x-y+3z-2=0 (Q): x+y+z-1=0 có phương trình là:
Trong không gian với hệ trục tọa độ Oxyz, phương trình của mặt phẳng (P) đi qua điểm B(2;1;-3), đồng thời vuông góc với hai mặt phẳng (Q): x+y+3z=0, (R): 2x-y+z=0 là
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d : x 2 = y - 3 1 = z - 2 1 và hai mặt phẳng
(P): x-2y+2z=0. (Q): x-2y+3z-5=0. Mặt cầu (S) có tâm I là giao điểm của đường thẳng d và mặt phẳng (P). Mặt phẳng (Q) tiếp xúc với mặt cầu (S). Viết phương trình của mặt cầu (S).
Trong không gian với hệ tọa độ Oxyz, cho điểm A(1;1;1) và hai mặt phẳng (P):2x-y+3z-1=0, (Q): y=0. Viết phương trình mặt phẳng chứa A, vuông góc với cả hai mặt phẳng và ?
A. 3x+y-2z-2=0
B. 3x-2z=0
C. 3x-2z-1=0
D. 3x-y+2z-4=0
Trong không gian với hệ trục tọa độ Oxyz, cho hai đường thẳng d 1 : x - 3 - 1 = y - 3 - 2 = z + 2 1 và d 2 : x - 5 - 3 = y + 1 2 = z - 2 1 và mặt phẳng (P) có phương trình x+2y+3z-5=0. Đường thẳng Δ vuông góc với (P) cắt d1 và d2 có phương trình là:
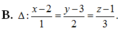
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng ∆ : x + 2 1 = y - 2 1 = z - 1 và mặt phẳng ( P ) : x + 2 y – 3 z + 4 = 0 . Phương trình tham số của đường thẳng d nằm trong (P), cắt và vuông góc đường thẳng ∆ là:
A. x = 1 - 3 t y = - 2 + 3 t z = - 1 + t
B. x = - 3 + 2 t y = 1 - t z = 1 + t
C. x = - 3 - 3 t y = 1 + 2 t z = 1 + t
D. x = - 3 + t y = 1 - 2 t z = 1 - t
Trong không gian với hệ trục tọa độ Oxyz, cho hai mặt phẳng P : x + m y + m - 1 z + 2 = 0 , Q : 2 x - y + 3 z - 4 = 0 . Giá trị số thực m để hai mặt phẳng (P); (Q) vuông góc
A. m = 1
B. m = - 1 2
C. m = 2
D. m = 1 2
Trong không gian với hệ tọa độ Oxyz, mặt phẳng (P) : x+my+3z+2=0 và mặt phẳng (Q): nx+y+z+7=0 song song với nhau khi
A. m=n=1
B. m = 3 ; n = 1 2
C. m = 3 ; n = 1 3
D. m = 2 ; n = 1 3
Trong không gian với hệ tọa độ Oxyz cho điểm A(3;-1;2) mặt phẳng (P): 4x-y+3z+2=0. Tính khoảng cách từ A đến (P).
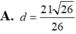
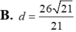
Trong không gian với hệ tọa độ Oxyz, cho điểm M(1;1;2) và mặt phẳng (P): 2x-y+3z+1=0. Đường thẳng đi qua điểm M và vuông góc với mặt phẳng (P) có phương trình
A. x + 1 2 = y + 1 - 1 = z + 2 3
B. x + 2 1 = y - 1 1 = z + 3 2
C. x - 2 1 = y + 1 1 = z - 3 2
D. x - 1 2 = y - 1 - 1 = z - 2 3
