Ta có:
d 1 : x - 1 2 = y 1 = z + 2 - 2 có 1 véc tơ chỉ phương là: u 1 → 2 , 1 , - 2
d 2 : x + 2 - 2 = y - 1 - 1 = z 2 có 1 véc tơ chỉ phương là: u 2 → - 2 , - 1 , 2
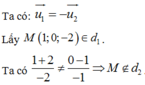
Vậy d 1 d 2 là hai đường thẳng song song
Chọn C
Ta có:
d 1 : x - 1 2 = y 1 = z + 2 - 2 có 1 véc tơ chỉ phương là: u 1 → 2 , 1 , - 2
d 2 : x + 2 - 2 = y - 1 - 1 = z 2 có 1 véc tơ chỉ phương là: u 2 → - 2 , - 1 , 2
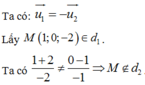
Vậy d 1 d 2 là hai đường thẳng song song
Chọn C
Trong không gian với hệ tọa độ Oxyz, xét vị trí tương đối của hai đường thẳng ∆ 1 : x - 1 1 = y 2 = z - 3 - 1 và ∆ 2 : x - 2 2 = y - 3 4 = z - 5 - 2
A. Trùng nhau
B. Song song
C. Chéo nhau
D. Cắt nhau
Trong không gian với hệ tọa độ Oxyz cho hai đường thẳng chéo nhau ∆ : x - 2 2 = y - 3 - 4 = z - 1 - 5 và d : x - 1 1 = y - 2 = z + 1 2 . Khoảng cách giữa hai đường thẳng ∆ và d bằng
A. 5 5
B. 45 14
C. 5
D. 3
Trong không gian với hệ trục tọa độ Oxyz, cho hai đường thẳng a : x 1 = y 1 = z - 2 ; b : x + 1 - 2 = y 2 = z + 1 - 1 và mặt phẳng ( P ) : x - y - z = 0 . Viết phương trình của đường thẳng d song song với (P), cắt a và b lần lượt tại M và N mà M N = 2 .
A. d : 7 x - 4 3 = 7 y + 4 8 = 7 z + 8 - 5
B. d : 7 x + 4 3 = 7 y - 4 8 = 7 z + 8 - 5 .
C. d : 7 x - 1 3 = 7 y - 4 8 = 7 z + 3 - 5
D. d : 7 x - 1 3 = 7 y + 4 8 = 7 z + 8 - 5
Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng chéo nhau d 1 : x - 2 2 = y + 2 1 = z - 6 - 2 và d 2 : x - 4 1 = y + 2 - 2 = z + 1 3 . Phương trình mặt phẳng (P) chứa đường thẳng d1 và song song với đường thẳng d2 là
A. (P): 2x + y - 6 = 0.
B. (P): x + 8y + 5z + 16 = 0.
C. (P): x + 4y + 3z - 12 = 0.
D. (P): x + 8y + 5z - 16 = 0.
Trong không gian với hệ trục tọa độ Oxyz , cho đường thẳng d có phương trình x = 6 + t y = - 2 - 5 t z = - 1 + t . Xét đường thẳng ∆ : x - a 5 = y - 1 - 12 = z + 5 - 1 , với a là tham số thực. Tìm tất cả các giá trị của a để đường thẳng d và ∆ cắt nhau.
A. a = 0
B. a = 4
C. a = 8
D. a = 1 2
Trong không gian với hệ trục tọa độ Oxyz, phương trình đường thẳng d : x - 1 2 = y + 2 1 = z - 1 song song với đường thẳng và cắt hai đường thẳng d 1 : x - 1 2 = y + 1 1 = z - 2 - 1 và d 2 : x - 1 2 = y - 2 1 = z - 3 3 là
A. ∆ : x + 1 - 1 = y + 1 1 = z - 2 1
B. ∆ : x - 1 1 = y 1 = z - 1 - 1
C. ∆ : x - 1 1 = y - 2 1 = z - 3 - 1
D. ∆ : x - 1 1 = y - 1 = z - 1 1
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): x - y - z - 1 = 0 và cho đường thẳng d : x + 1 2 = y - 1 1 = z - 2 3 , cho A(1; 1; -2). Viết phương trình đường thẳng đi qua A, song song với (P) và vuông góc với d
A. x - 1 2 = y - 1 5 = z + 2 3
B. x - 1 2 = y - 1 - 5 = z 2
C. x - 1 2 = y - 1 - 5 = z + 2 - 3
D. x - 1 2 = y - 1 5 = z + 2 - 3
Trong hệ tọa độ Oxyz, cho hai đường thẳng chéo nhau d 1 : x − 2 2 = y + 2 1 = z − 6 − 2 v à d 2 : x − 4 1 = y + 2 − 2 = z + 1 3 . Phương trình mặt phẳng (P) chứa d 1 và song song với d 2 là:
A. P : x + 8 y + 5 z + 16 = 0
B. P : x + 8 y + 5 z − 16 = 0
C. P : 2 x + y − 6 = 0
D. P : x + 4 y + 3 z − 12 = 0
Trong không gian với hệ trục tọa độ Oxyz, cho ba đường thẳng d 1 : x - 3 2 = y + 1 1 = z - 2 - 2 , d 2 : x + 1 3 = y - 2 = z + 4 - 1 và d 3 : x + 3 4 = y - 2 - 1 = z 6 . Đường thẳng d 3 song song , cắt d 1 và d 2 có phương trình là:
A. △ : x - 3 4 = y + 1 1 = z - 2 6
B. △ : x - 3 - 4 = y + 1 1 = z - 2 - 6
C. △ : x + 1 4 = y - 1 = z - 4 6
D. △ : x - 1 4 = y - 1 = z + 4 6