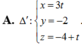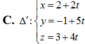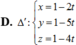Trong không gian với hệ tọa độ Oxyz, cho đường thẳng ∆ : x + 2 1 = y - 2 1 = z - 1 và mặt phẳng ( P ) : x + 2 y - 3 z + 4 = 0 . Đường thẳng d nằm trong (P) sao cho d cắt và vuông góc với ∆ có phương trình là:
A. x + 3 1 = y - 1 - 1 = z - 1 2
B. x + 1 - 1 = y - 3 2 = z + 1 1
C. x - 3 1 = y + 1 - 1 = z + 1 2
D. x + 3 - 1 = y - 1 2 = z - 1 1
Đáp án D.
Đường thẳng ∆ có vecto chỉ phương u ∆ → = 1 ; 1 ; - 1 .
Một mặt phẳng P có vecto pháp tuyến n p → = 1 ; 2 ; 3
Gọi I = ∆ ∩ P , tọa độ I là nghiệm của hệ phương trình:
x + 2 1 = y - 2 1 = z - 1 x + 2 y - 3 z + 4 = 0 ⇒ I - 3 ; 1 ; 1
Do d ⊂ P d ∩ ∆ ≢ ∅ ⇒ I ∈ d và d ⊂ P d ⊥ ∆
⇒ Đường thẳng d có một vecto chỉ phương u d → = u ∆ → , n P → = - 1 ; 2 ; 1
Vậy d : x + 3 - 1 = y - 1 2 = z - 1 1 .