Trong không gian với hệ tọa độ Oxyz cho điểm A(0;1;2) mặt phẳng α : x - y + z - 4 = 0 và S : x - 3 2 + y - 1 2 + z - 2 2 = 16 . Gọi (P) là mặt phẳng đi qua A vuông góc với α và đồng thời (P) cắt mặt cầu (S) theo giao tuyến là một đường tròn có bán kính nhỏ nhất. Tọa độ giao điểm M của (P) và trục xOx' là
A. M - 1 3 ; 0 ; 0
B. M 1 ; 0 ; 0
C. M - 1 2 ; 0 ; 0
D. M 1 3 ; 0 ; 0
Mặt phẳng là mặt phẳng đi qua A(0;1;2) và có VTPT ![]()
Khi đó ![]()
• (P) vuông góc với α nên: a - b + c = 0
• (P) cắt mặt cầu (S) theo giao tuyến là một đường tròn có bán kính nhỏ nhất khi và chỉ khi khoảng cách từ tâm mặt cầu đến mặt phẳng (P) là lớn nhất. Ta có
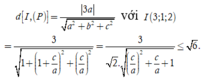
Dấu "x" xảy ra ![]()
Chọn c = -1, suy ra ![]()
Khi đó ![]()
Chọn C.

