Trong không gian với hệ tọa độ Oxyz, cho các điểm A a ; 0 ; 0 , B 0 ; b ; 0 , C 0 ; 0 ; c với a,b,c dương. Biết A, B, C di động trên các tia O x , O y , O z sao cho a + b + c = 2 . Biết rằng khi a,b,c thay đổi thì quỹ tích tâm hình cầu ngoại tiếp tứ diện OABC thuộc mặt phẳng (P) cố định. Tính khoảng cách từ M 2016 ; 0 ; 0 tới mặt phẳng (P).
A. 2017
B. 2014 3 .
C. 2016 3 .
D. 2015 3 .
Đáp án D
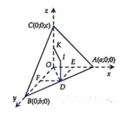
Gọi D, K lần lượt là trung điểm của AB, OC.
Từ D kẻ đường thẳng vuông góc với mặt phẳng O A B và cắt mặt phẳng trung trực OC tại I x 1 ; y 1 ; z 1 suy ra I là tâm mặt cầu ngoại tiếp tứ diện OABC và z 1 = c 2 (do DOKI là hình chữ nhật).
Tương tự D F = a 2 ⇒ x 1 = a 2 ; y 1 = b 2 ⇒ I a 2 ; b 2 ; c 2 .
Suy ra x 1 + y 1 + z 1 = a + b + c 2 = 1 ⇒ I ∈ P : x + y + z − 1 = 0 .
Vậy khoảng cách từ điểm M đến (P) là d = 2015 3 .

