Đáp án D
Phương pháp giải: Xét đẳng thức vectơ, đưa về hình chiếu của điểm trên mặt phẳng
Lời giải:
Gọi M(a;b;c) thỏa mãn đẳng thức vectơ 2 M A → + M B → + M C → = 0 →
![]()
![]()
![]()
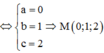
Khi đó S = 2 N A 2 + N B 2 + N C 2 = 2 N A 2 → + N B 2 → + N C 2 → = 2 M N → + M A → 2 + M N → + M B → 2 + M N → + M C → 2
= 4 M N 2 + 2 N M → 2 M A → + M B → + M C → + 2 M A 2 → + M B 2 → + M C 2 →
= 4 M N 2 + 2 M A 2 → + M B 2 → + M C 2 →
Suy ra Smin ó MNmin ó N là hình chiếu của M trên(P) => MN ⊥ (P)
Phương trình đường thẳng MN là 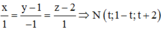
Mà m ∈ mp(P) suy ra t–(1–t)+t+2+2=0 ó t = –1 => N(–1;2;1)

