Đáp án C.
Ta có x + y + z = 3 ⇔ x 3 + y 3 + z 3 = 1 . Suy ra tập hợp các điểm M x ; y ; z là 8 mặt chắn có phương trình: ;
x 3 + y 3 + z 3 = 1 ; x − 1 + y − 3 + z − 3 = 1 ; x − 3 + y − 3 + z 3 = 1
x − 3 + y 3 + z − 3 = 1 ; x 3 + y − 3 + z − 3 = 1 ; x − 3 + y 3 + z 3 = 1 ; x 3 + y − 3 + z 3 = 1 ; x 3 + y 3 + z − 3 = 1
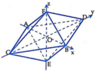
Các mặt chắn này cắt các trục Ox, Oy, Oz tại các điểm , A − 3 ; 0 ; 0 , B 3 ; 0 ; 0 , C 0 ; − 3 ; 0 D 0 ; 3 ; 0 , E 0 ; 0 ; − 3 , F 0 ; 0 ; 3 .
Từ đó, tập hợp các điểm M x ; y ; z thỏa mãn x + y + z = 3 là các mặt bên của bát diện đều x + y + z = 3 (hình vẽ) cạnh bằng 3 2 .
Thể tích khối bát diện đều là V = 3 2 3 . 2 3 = 36 (đvtt).

