Đáp án B
Phương pháp :
Gọi A(a;0;0), B(0;b;0), C(0;0;c) (a;b;c>0) => OA = a; OB = b; OC = c
Viết phương trình mặt phẳng (P): x a + y b + z c = 1
Cách giải :
Gọi A(a;0;0), B(0;b;0), C(0;0;c) (a;b;c>0) => OA = a; OB = b; OC = c
O
A
1
=
O
B
2
=
O
C
4
<=> 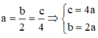
Khi đó phương trình mặt phẳng (P) là: x a + y 2 a + z 4 a = 1
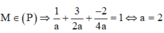
Vậy phương trình mặt phẳng (P) là :
x 2 + y 4 + z 8 = 1 <=> 4x + 2y + z – 8 = 0

