Các câu hỏi tương tự
Trong không gian Oxyz, cho hai điểm A(2; 0; 1), B(8; 4; -5) và mặt phẳng 2x + 2y - z + 1 0. Tìm tọa độ của điểm M thuộc mặt phẳng (P) sao cho
AM
2
+
BM
2
đạt giá trị nhỏ nhất A. M(1; -2; -1) B. M(9; 6; -5) C. M(1; -2; -5) D. Đáp án khác
Đọc tiếp
Trong không gian Oxyz, cho hai điểm A(2; 0; 1), B(8; 4; -5) và mặt phẳng 2x + 2y - z + 1 = 0. Tìm tọa độ của điểm M thuộc mặt phẳng (P) sao cho AM 2 + BM 2 đạt giá trị nhỏ nhất
A. M(1; -2; -1)
B. M(9; 6; -5)
C. M(1; -2; -5)
D. Đáp án khác
Trong mặt phẳng tọa độ Oxy cho đường thẳng d 4x+2y+1=0 và điểm A(1;1)
Xác định tọa độ hình chiếu vuông góc của Alên d.
Trong không gian Oxyz, lập phương trình chính tắc của đường thẳng d đi qua điểm M(0;1;-1), nằm trong mặt phẳng (P): x + 2y + z - 1 0 và vuông góc với đường thẳng A.
d
:
x
9
y
-
1
-
2
z
+
3...
Đọc tiếp
Trong không gian Oxyz, lập phương trình chính tắc của đường thẳng d đi qua điểm M(0;1;-1), nằm trong mặt phẳng (P): x + 2y + z - 1 = 0 và vuông góc với đường thẳng 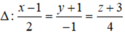
A. d : x 9 = y - 1 - 2 = z + 3 4
B. d : x 9 = y - 1 2 = z + 1 5
C. d : x 9 = y + 1 - 2 = z - 1 - 5
D. d : x 9 = y + 1 2 = z - 1 - 5
trong mặt phẳng hệ tọa độ Oxy cho hình thang cân ABCD có hai đường chéo BD và AC vuông góc với nhau tại H và AD 2 BC. Gọi M là điểm nằm trên cạnh AB sao cho AB 3 AM N là trung điểm HC. biết B 1 3 đường thẳng HM đi qua T 2 3 đường thẳng DN có phương trình x 2y 2 0 . tìm tọa độ các điểm A,C,D
Cho đường thẳng d: x - 2y - 3 = 0. Tọa độ hình chiếu vuông góc H của điểm M(0;1) trên đường d là:
A. H(-1;2)
B. H(5;1)
C. H(3;0)
D. H(1;-1)
Trong không gian Oxyz, phương trình chính tắc của đường thẳng d đi qua điểm M(-1;-2;3) và vuông góc với mặt phẳng (P): x - 2y + 3z - 1 0 A.
x
-
1
1
y
-
2
-
2
z
+
3...
Đọc tiếp
Trong không gian Oxyz, phương trình chính tắc của đường thẳng d đi qua điểm M(-1;-2;3) và vuông góc với mặt phẳng (P): x - 2y + 3z - 1 = 0
A. x - 1 1 = y - 2 - 2 = z + 3 3
B. x - 1 - 1 = y + 2 - 2 = z - 3 3
C. x + 1 - 1 = y - 2 - 2 = z + 3 3
D. x + 1 1 = y + 2 - 2 = z - 3 3
Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(2;4), trọng tâm G ( 2 ; 2 3 ) . Biết rằng đỉnh B nằm trên đường thẳng d: x + y + 2 = 0 và đỉnh C có hình chiếu vuông góc trên d là điểm H(2;-4). Giả sử B(a;b). Tính giá trị của biểu thức P = a - 3b.
Trong mặt phẳng tọa độ oxy cho hình thang ABCD vuông tại A và D có CD = 2AB và B ( 2;3 ), gọi E là trung điểm của cạnh CD, H là hình chiếu vuông góc của E lên AC, biết phương trình đường thẳng DH: x + 2y -3 = 0 và đường thẳng AC di qua k ( 1;3 )
Điểm H là hình chiếu vuông gòc của M(3;-2) trên d:2x-3y+1=0. Khi đó


