Dễ thấy BC → ⊥ AC → , BC ' → ⊥ AC → ' , BB ' → ⊥ AB → ' nên A, B, C, B', C' cùng thuộc mặt cầu tâm I(1/2; 1; 0) là trung điểm của AB, bán kính IA = ( 5 ) /2
Phương trình mặt cầu đó là
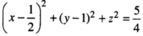
Vì điểm C' thuộc mặt cầu, nên mặt phẳng tiếp xúc với mặt cầu tại C' phải vuông góc với IC ' → = (-1/2; 0; 1). Phương trình của mặt phẳng đó là: x - 2(z - 1) = 0 hay x - 2z + 2 = 0

